技术摘要：
本发明涉及穿墙雷达技术领域，尤其是一种穿墙雷达目标近墙机动跟踪方法，本发明提出了一种新的运动惯性模型，即协方差预测公式不但与历史信息有关，而且与转向程度有关，即：转向角越小，预测方式越接近线性卡尔曼滤波方式；转向角越大，历史信息的影响越小；采取该预  全部
背景技术：
在反恐处突、消防救援等任务中，穿墙雷达是一种有效探测墙后人体目标的设备， 但由于电磁波穿透墙体衰减很大，而且墙后房屋结构、家具等环境复杂，因此对目标的检测 和跟踪方法的要求很高。 在穿墙雷达目标跟踪技术上，目标近墙机动的跟踪是难点和关键之一，目标近墙 机动是指人员在室内运动时，接近墙体的时候快速机动转向的过程。近墙机动的目标跟踪 的主要难点在于： (1)目标在接近墙体之前必然会快速转向，转向角度至少大于90°，且转向时间短， 机动性强； (2)目标接近墙体的时候，由于多径效应严重，墙体会出现虚假目标，造成目标关 联错误； (3)目标在转向机动过程中，速度会有短暂降低的时间段，多普勒频移接近为0，根 据雷达动目标检测原理，此时目标会偶尔丢失。 因为上述原因，目标近墙机动过程中对其进行跟踪的难度很大，也是穿墙雷达目 标跟踪的难点和关键所在。 现有技术的缺点：在传统跟踪模型上穿墙雷达在目标近墙运动探测时，易于出现 目标虚警和漏警的问题。 近墙跟踪是穿墙雷达跟踪的难点和关键，传统的跟踪一般采用卡尔曼滤波模型进 行跟踪计算。 传统卡尔曼滤波模型假设k时刻的真实状态是从k-1时刻的状态演化而来，符合下 式： xk＝Fkxk-1 Bkuk wk 其中： Fk是作用在xk-1上的状态变换模型； Bk是作用在控制器向量uk上的输入-控制模型； wk是过程噪声，并假定其符合均值为零，协方差矩阵为Qk的多元正态分布，即wk～N (0，Qk)。 在时刻k，对真实状态xk的一个测量zk满足下式： zk＝Hkxk vk 其中：Hk是观测模型，它把真实状态空间映射成观测空间，vk是观测噪声，其均值为 0，协方差矩阵为Rk，且服从正态分布，即vk～N(0，Rk)。并且初始状态以及每一时刻的噪声 {x0，w1，...，wk，v1...vk}都认为是互相独立的。 卡尔曼滤波是一种递归的估计，即只要获知上一时刻状态的估计值以及当前状态 3 CN 111596291 A 说　明　书 2/5 页 的观测值就可以计算出当前状态的估计值，因此不需要记录观测或者估计的历史信息。卡 尔曼滤波器与大多数滤波器不同之处，在于它是一种纯粹的时域滤波器，它不需要像低通 滤波器等频域滤波器那样，需要在频域设计再转换到时域实现。 卡尔曼滤波器的状态由以下两个变量表示： (1) 在时刻的状态的估计； (2)Pk|k，后验估计误差协方差矩阵，度量估计值的精确程度。 卡尔曼滤波器的操作包括两个阶段：预测与更新。 在预测阶段，滤波器使用上一状态的估计，做出对当前状态的估计。预测阶段的预 测状态 和预测估计协方差矩阵P分别为： 在更新阶段，滤波器利用对当前状态的观测值优化在预测阶段获得的预测值，以 获得一个更精确的新估计值。首先要算出以下测量余量 测量余量协方差Sk和最优卡尔 曼增益Kk： 然后用它们来更新滤波器变量状态估计x与协方差P： Pk|k＝(I-KkHk)Pk|k-1 对于二维X-Y空间的人员目标，其k时刻坐标、速度和加速度可表示为： 其中 和 和 和 分别为k时刻目标的X和Y坐标值、X和Y方向上的速 度分量，以及X和Y方向上的加速度分量。特别有 其中T为相邻两次测量的间隔。根据牛顿运动定律，k 1时刻的目标位置可估计为 4 CN 111596291 A 说　明　书 3/5 页 此时，k时刻卡尔曼滤波器中的状态向量、测量向量和状态变换矩阵、测量模型矩 阵为 xk＝[pk  vk  ak]T Hk＝[1  1  0  0  0  0] 由人体一般运动规律可知，在非快速机动条件下，人体目标的速度和加速度在相 邻测量时间内可以近似为不变，即保持匀速直线运动，因此上述线性卡尔曼滤波满足人体 运动情况。 但在近墙机动过程中，由于快速转向使得相邻测量参数的相关性急剧降低，依靠 历史信息无法对当前目标位置进行正确滤波，从而无法准确预测之后的目标位置。
技术实现要素：
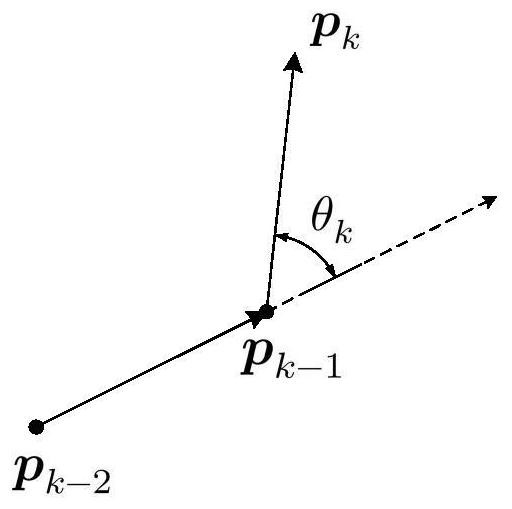
本发明要解决的技术问题是：本发明提出了一种新的运动惯性模型，即协方差预 测公式不但与历史信息有关，而且与转向程度有关，即：转向角越小，预测方式越接近线性 卡尔曼滤波方式；转向角越大，历史信息的影响越小；采取该预测策略，将有效降低快速转 向时跟踪失效的概率。 一种穿墙雷达目标近墙机动跟踪方法,提出了一种新的运动惯性模型， 步骤1：根据k时刻相邻两次测量间的转向角度θk，计算修正因子mk为 步骤2：通过mk，依据新的协方差预测公式为： 计算运动目标的参数信息。 具体的， (1)当目标直线运动时，θk＝0，从而mk＝0， 预测公式 退化为线性卡尔曼滤波模型； (2)当目标调头运动时，θk＝π，从而mk＝1，Pk|k-1＝P0 Qk，预测公式退化为线性卡尔 曼滤波模型。 具体的，该运动惯性模型与目标运动的历史信息有关。 具体的，该运动惯性模型与目标运动的转向程度有关。 具体的，该运动惯性模型中目标运动的转向角越小，预测方式越接近线性卡尔曼 滤波方式。 具体的，该运动惯性模型中目标运动的转向角越大，受目标运动历史信息的影响 越小。 具体的，该运动惯性模型中目标运动的转向角越大，其修正因子mk越大，mk被初始 5 CN 111596291 A 说　明　书 4/5 页 化。 本发明的协方差预测公式为： 其中P0为初始协方差，mk为k时刻的修正因子，且有mk∈[0，1]。可以看出，当mk取极 限值时： (1)mk＝0，协方差预测公式与传统线性卡尔曼模型相同； (2)mk＝1，协方差Pk被替换为初始化值P0。 即转向机动越剧烈，mk越大，从而Pk-1影响越小；特别时当目标突然调头行进时，此 时mk＝1，Pk被初始化。因此，mk应该与转向角度密切相关，且在[0，π]区间内单调递增。 本专利定义修正因子mk为 其中θk为k时刻相邻两次测量间的转向角度， 对应θk两种极限取值情况为： (1)当目标直线运动时，θk＝0，从而mk＝0， 预测公式 退化为线性卡尔曼滤波模型； (2)当目标调头运动时，θk＝π，从而mk＝1，Pk|k-1＝P0 Qk，预测公式退化为线性卡尔 曼滤波模型。 修正因子mk与转向角度θk的公式mk(θk)也可以采用其他形式，但必须要保证随θk在 [0，π]内增加时mk在[0，1]内单调递增。 本发明的有益效果： (1)提高了目标近墙机动时运动方向判断的准确率，保证目标跟踪的有效性和可 靠性； (2)在非剧烈机动情况下，保持了常规卡尔曼滤波器的良好跟踪滤波性能。 附图说明 图1是本发明的k时刻相邻两次测量间的转向角度为θk示意图；