技术摘要：
本发明公开了一种基于非凸张量范数和全变分的高光谱图像恢复方法，包括获取带噪的高光谱图像数据，建立高光谱图像噪声的数学模型；构造加权邻域均值三维全变分，构建基于加权截断张量Schatten‑p范数和加权邻域均值三维全变分的高光谱图像恢复模型WTTS‑WTDTV；引入辅  全部
背景技术：
随着高光谱成像技术的出现和近三十年的迅速发展，高光谱遥感已经成为空间遥 感领域的关键技术，被广泛应用于地质勘探、农业遥测、水文监视和军事探测等重要领域。 由于大气干扰，传感器精度等各种因素，高光谱图像(HIS)在获取过程中有可能会 受到高斯噪声、脉冲噪声和条带噪声等的影响。由于应用范围十分广泛，去噪成为在HSI后 续应用前必不可少的预处理步骤。 围绕高光谱图像的去噪问题，国内外研究者们提出了很多的去噪方法，已有的高 光谱图像去噪办法主要分为三类：第一类是基于滤波的去噪方法。基于滤波的高光谱图像 去噪技术通常使用三维滤波，或在光谱/空间其中一个维度进行滤波去噪，另外维度使用其 他方法去噪。第二类是基于低秩表示的方法。考虑到高光谱图像的三维结构，张量和多重线 性代数常常被用于高光谱图像的低秩近似。第三类是基于全变分的方法。全变分(Total  variation，TV)的图像去噪方法，其思想是无噪声的图像应具有平滑性，故其全变分范数较 小，而噪声成分的存在会使得全变分范数变大。将带噪声图像通过全变分范数正则化，即可 将噪声去除。基于TV的去噪算法能很好处理成片光滑的高光谱图像，但用于细节较多的高 光谱图像，容易导致细节丢失。
技术实现要素：
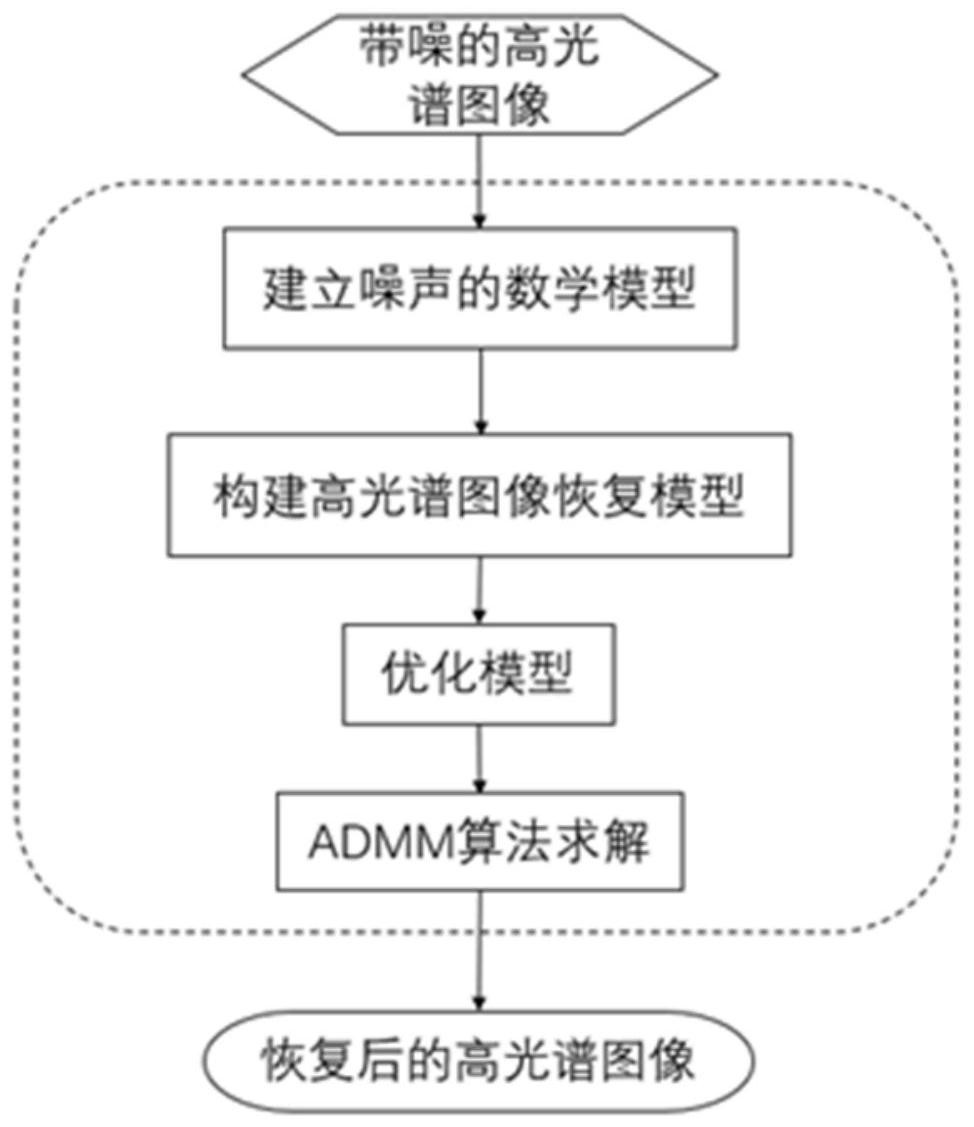
本申请的目的是提供一种基于非凸张量范数和全变分的高光谱图像恢复方法，可 以进一步提高高光谱图像恢复的效果，具体的是一种基于加权截断张量Schatten-p范数和 加权邻域均值三维全变分的高光谱图像恢复方法，简称为WTTS-WTDTV。 为了实现上述目的，本申请技术方案如下： 一种基于非凸张量范数和全变分的高光谱图像恢复方法，其特征在于，所述方法 包括以下步骤： 步骤1、获取带噪的高光谱图像数据，建立高光谱图像噪声的数学模型； 步骤2、构造加权邻域均值三维全变分，构建基于加权截断张量Schatten-p范数和 加权邻域均值三维全变分的高光谱图像恢复模型； 步骤3、为消除矩阵之间的相关性，引入辅助矩阵，优化所述高光谱图像恢复模型； 步骤4、采用ADMM算法求解优化后的高光谱图像恢复模型，获得降噪后的恢复图 像； 其中，所述高光谱图像噪声的数学模型为： 表示干净的高光谱图 像， 表示带噪的高光谱图像， 表示稀疏噪声， 表示高密度噪声； 所述构造加权邻域均值三维全变分，构建基于加权截断张量Schatten-p范数和加 5 CN 111598797 A 说　明　书 2/8 页 权邻域均值三维全变分的高光谱图像恢复模型，包括： 首先，定义图像的邻域均值差分运算： 其中，m,n分别表示高光谱图像在空间维度上的长和宽，h代表其在光谱维度上的 波段数， 表示实数，(i,j ,k)表示图像 对应的沿空间长度、宽度和谱段方向的坐标位 置， 表示图像在位置(i,j,k)沿水平、垂直和光谱方向的差分运算之 后得到的梯度值， 表示图像在位置的灰度值， 和 表示对应图像 在位置(i,j,k)沿着空间长度、宽度和谱段方向平移一个位置的像素灰度值； 进而构造邻域均值差分操作算子Gs(·)， Gs(·)＝[ρvGv(·)；ρtGt(·)；ρzGz(·)] 其中，Gv(·)、Gt(·)和Gz(·)分别表示水平、垂直和光谱三个不同方向的差分操 作，ρs(s＝v,t,z)是用来控制对三个维度的约束强度的参数。 从而得到加权邻域均值三维全变分： 其中，wi,j,k是位置(i,j,k)上图像的梯度值权重； 所述加权邻域均值三维全变分可以简写为： 其中，⊙ 是外积算子，W是权重矩阵，||·||1表示张量的 L1范数； 然后再定义所述的加权截断张量Schatten-p范数： 其中，r为截断阈值，p(0≤p≤1)为Schatten-p范数的参数， 是张量 的i-模的 展开矩阵， 是矩阵 的第j个奇异值且满足σr 1≥σr 2≥…≥σmin (m ,n)≥0。 6 CN 111598797 A 说　明　书 3/8 页 是对应奇异值的权重参数，ωi是权重ω的第i个元素； 利用 所述加权截断张量Schatten-p范数改写 为： 其中， 和 分别为张量 的t-SVD分解生成的左奇异特征张量 和右奇异特征张量； 从而构建基于加权截断张量Schatten-p范数和加权邻域均值三维全变分的高光 谱图像恢复模型： 其中，τ是调整加权邻域均值三维全变分的参数，λ是限制稀疏噪声的稀疏性参数。 表示L2，1范数，||·||F表示张量的Frobenius范数，ε是一个常数，表示高 密度噪声的标准偏差。 进一步的，所述为消除矩阵之间的相关性，引入辅助矩阵，优化所述高光谱图像恢 复模型，包括： 为消除矩阵 之间的相关性，引入辅助矩阵 和V1,V2,V3，得到所述的恢复优化 模型： 进一步的，所述采用ADMM算法求解优化后的高光谱图像恢复模型，获得降噪后的 恢复图像，包括： 步骤4.1、采用ADMM算法求解优化后的高光谱图像恢复模型，固定其它变量，更新 7 CN 111598797 A 说　明　书 4/8 页 式中，u是惩罚参数，Λ1,Λ2Λ3,Λ4,Λ5是拉格朗日乘子； 步骤4.2、固定其它变量，更新 步骤4.3、固定其它变量，更新V (k 1)1 ： 步骤4.4、固定其它变量，更新V (k 1)2 ： 步骤4.5、固定其它变量，更新V (k 1)3 ： 步骤4.6、固定其它变量，更新 步骤4.7、固定其它变量，更新拉格朗日乘子： 步骤4.8、判断是否满足迭代终止条件，若 其中 表示张 量 的所有元素的平方和，则终止迭代，输出无噪的图像 否则，继续迭代更新。 本申请提出的基于非凸张量范数和全变分的高光谱图像恢复方法，具有如下有益 效果： (1)该方法能有效去除高斯噪声、稀疏噪声和混合噪声； (2)能有效利用干净的高光谱图像的低秩张量特性； 8 CN 111598797 A 说　明　书 5/8 页 (3)考虑了空间维度和光谱维度之间的一致性； (4)能有效利用光谱信息，在去噪的同时，避免由此引起的光谱失真情况。 附图说明 图1为本申请实施例基于非凸张量范数和全变分的高光谱图像恢复方法流程图。