技术摘要：
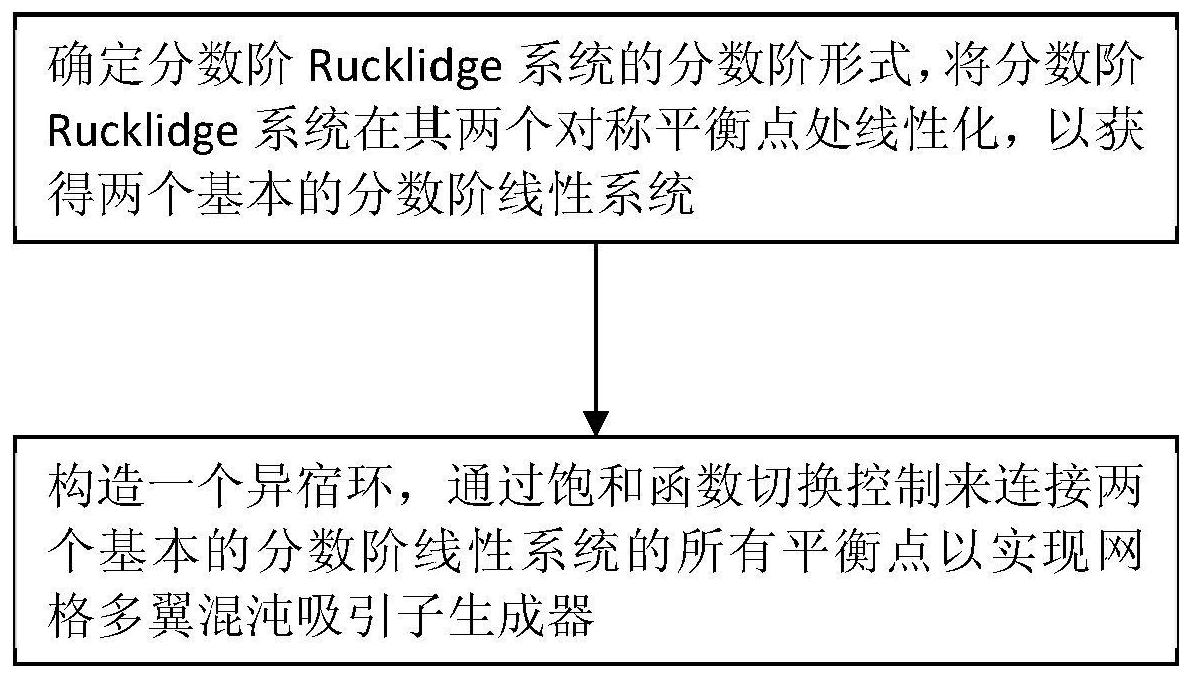
本发明公开了一种分数阶微分系统构造网格多翼混沌吸引子生成器的方法，包括以下步骤：步骤一：确定分数阶Rucklidge系统的分数阶形式，将分数阶Rucklidge系统在其两个对称平衡点处线性化，以获得两个基本的分数阶线性系统；步骤二：构造一个异宿环，通过饱和函数切换控  全部
背景技术：
分数阶微积分是300多年来的经典数学概念。但是它在物理和工程应用中的应用 只是最近受到关注的主题。最近，许多研究人员惊奇地发现，许多分数阶非线性微分系统也 可以显示复杂的分叉和混沌现象。例如，分数阶蔡氏电路也有一个双涡卷混沌吸引子。艾哈 迈德(Ahmad)引入了一种从分数阶系统创建n个混沌吸引子的阶跃函数方法，设计了一种基 于分数阶微分系统通过切换控制的多方向多涡卷混沌吸引子。有人通过耦合两个分数阶洛 伦兹系统获得的分数阶系统中产生四翼混沌吸引子。此外，还有人提出了通过分数阶线性 差分系统生成多翼混沌吸引子的方法，该方法是通过配备对偶对称多段二次函数的非线性 状态反馈控制器进行的。然而，分数阶系统中的网格多翼混沌吸引子的设计仍是一个非常 具有挑战性的问题。
技术实现要素：
为了解决上述技术问题，本发明提供一种算法简单的分数阶微分系统构造网格多 翼混沌吸引子生成器的方法。 本发明解决上述问题的技术方案是：一种分数阶微分系统构造网格多翼混沌吸引 子生成器的方法，包括以下步骤： 步骤一：确定分数阶Rucklidge系统的分数阶形式，将分数阶Rucklidge系统在其 两个对称平衡点处线性化，以获得两个基本的分数阶线性系统； 步骤二：构造一个异宿环，通过饱和函数切换控制来连接两个基本的分数阶线性 系统的所有平衡点以实现网格多翼混沌吸引子生成器。 上述分数阶微分系统构造网格多翼混沌吸引子生成器的方法，所述步骤一中，确 定分数阶Rucklidge系统的分数阶形式的过程为： 分数阶微分方程为： 其中，Dt表示对t求偏导数；x(t)、y(t)、z(t)均为状态变量；t为时间变量；f1、f2、f3 分别表示x(t)、y(t)、z(t)对t的偏导数函数；T为最大时间值；αi为阶数；初始值x(0)＝x0,y (0)＝y0,z(0)＝z0,αi∈(0,1)(i＝1,2,3)，因此，式(1)等效于Volterra积分方程： 7 CN 111582490 A 说　明　书 2/11 页 其中τ为积分变量；GammaΓ(αi)函数定义为 设置 tn＝ nh，n＝0,1,2,KN，h为每一段时间间隔的长度；tn为第n段时间间隔；N为时间间隔个数最大 值；n为0—N之间的整数，则式(2)离散为： 其中，xh(tn 1)为状态变量在第n 1段时间间隔的离散值； 为状态变量在第n 1段时间间隔的预测值；αi,k,n 1为第n 1段时间间隔的迭代系数；x(tk)为在tk时刻状态变量 x的值； αi ,k ,n 1为： 当k 超出范围时，αi,k,n 1＝1； 预测值取决于： 其中b1 ,k,n 1、b2,k,n 1、b3,k,n 1分别为α1、α2、α3阶状态变量x的迭代系数；f1(xh(tk))、 f2(xh(tk))、f3(xh(tk))分别为f1、f2、f3函数在自变量取tk时刻状态变量x的离散值时所对应 的函数值； 式(4)的估计误差为e ＝max{max|x(tk)-xh(tk)|,max|y(tk)-yh(tk)|,max|z(tk)-zh(tk)|}＝o(hρ)，o(hρ)表示hρ的 高阶无穷小，ρ为中间变量，k＝(0,1,2,K,N) ,ρ＝min{1 α1,1 α2,1 α3}； 确定分数阶系统的数值解，得到Rucklidge系统的分数阶形式为： 8 CN 111582490 A 说　明　书 3/11 页 上述分数阶微分系统构造网格多翼混沌吸引子生成器的方法，所述步骤一中，获 得两个基本的分数阶线性系统的过程为： 针对分数阶αi(i＝1,2,3)，满足0<αi≤1，显然，系统(5)具有三个平衡点：第一平衡 点E0＝(0,0,0)，第二平衡点 第三平衡点 在E1处线性 化系统(5)，得到以下分数阶线性系统： 类似地，在E2处的线性化系统(5)，得到以下分数阶线性系统： J1、X1、J2、X2均为中间变量； 以下，将系统(6)和(7)称为基本分数阶线性系统；显然，O0＝O1＝(0,0,0)是系统 (6)和(7)的唯一平衡点，并且对应的特征值是λ1＝γ＝-3.5145和λ2,3＝σ±jω＝0.2577± j1.9353；λ1、λ2,3为系统(6)和(7)对应的三个特征值；γ、σ表示特征值的实部；ω表示特征 值的虚部；因此，平衡点O1,O2都是指标2的鞍焦点，而且λ1<0,Re(λ2,3)>0,Re(λ2,3)表示特征值 λ2,3的实部，|λ1|>Re(λ2,3) ,满足Shil'nikov定理的条件；如果所有平衡点的雅可比矩阵特征 值满足以下条件，则它们在局部渐近稳定： |arg(eig(JF))|>αiπ/2    (8) JF为雅可比矩阵； 不等式(8)表明，分数阶微分方程组比其整数阶方程组更稳定； 更改αi<1(i＝1,2 ,3)的值时，系统(6)和(7)并不总是保持混乱；从不等式(4)开 始，系统(6)保持混沌的必要条件是，在不稳定区域的每个非原点的平衡点处保持雅可比矩 阵的两个共轭特征值，这意味着对于i＝1,2,3, 此外，对应的 特征向量如下所示： 9 CN 111582490 A 说　明　书 4/11 页 η1、μ1、η2、μ2均表示特征向量，实数形式的用η表示，复数形式的用μ表示；通过计 算，得出系统(6)的一维稳定本征线ES(O1)和二维不稳定本征面EU(O1)如下： 这里中间变量l1＝-0.8381,m1＝0.2384,n1＝-0.4907,A1＝-0.1911,B1＝0.2895, C1＝-0.1966； 同样，获得系统(7)的一维稳定本征线ES(O2)和二维不稳定本征面EU(O2)如下： 这里中间变量l2＝-0.8381,m2＝0.2384,n2＝0.4907,A2＝0.1911,B2＝-0.2895,C2 ＝-0.1966；显然，稳定的本征线ES(O )、ES(O )和不稳定的本征面EU(O )、EU1 2 1 (O2)分别在一定 程度上对称。 上述分数阶微分系统构造网格多翼混沌吸引子生成器的方法，所述步骤二具体过 程为： 基于基本分数阶线性系统(6)和(7)，扩展Shil'nikov定理，设计一种切换控制器 来连接系统(6)和(7)的异宿轨道以形成异宿环，涉及过程为：设交换平面为S＝{(x,y,z)|y ＝0}，切换控制器为w＝F(x,y,z)，从系统(6)和系统(7)，构造以下可切换系统： 其中，X：表示列矩阵 V泛指三维空间；V1指三维空间中y>0的那部分子空间；V2 指三维空间中y<0的那部分子空间； 开关控制器w＝F(x,y,z)＝[f1(x,y,z) ,f2(x,y,z) ,f3(x,y,z)]T的详细数学表达 10 CN 111582490 A 说　明　书 5/11 页 式由系统(11)中的异宿回路的存在条件决定；显然，系统(11)的两个平衡点P1(x1,y1,z1)∈ V1和P2(x2,y2,z2)∈V2分别位于开关平面S＝{(x,y,z)|y＝0}的两侧；其中ES(P1)和EU(P1)是 系统(6)在P1处的本征线和本征面，ES(P U2)和E (P2)是系统(7)在P2处的本征线和本征面，表 示为： L ＝EU1 (P1)∩S＝A1(x-x1) B1(0-y1) C1(z-z1)＝0, L ＝EU2 (P2)∩S＝A2(x-x2) B2(0-y2) C2(z-z2)＝0 其中，Q 为本征线ES1 (P1)与平面S的相交点；Q S2为本征线E (P2)与平面S的相交点；L1 为本征面EU(P1)与平面S的相交线；L2为本征面EU(P2)与平面S的相交线； 如果Q1位于L2，则存在一个从P2到P1的异宿轨道H1＝EU(P2)∪Q1∪ES(P1)；同样，如 果Q 位于L ，则存在一个从P 到P 的异宿轨道H ＝EU(P )∪Q ∪ES2 1 1 2 2 1 2 (P2)；因此，如果Q1位于L2和 Q2位于L1，则存在一个由两个异宿轨道组成并相互连接的异宿环H1和H2连接P1和P2，在这种 情况下，根据Shil'nikov定理，系统(6)在Smale马蹄形意义上是混乱的； 从变换(x，y，z)→(-x，-y，z)的不变性，选择开关平面S＝{(x,y,z)|y＝0}，该平面 满足P1(x1,y1,z1)∈V1,P2(x2,y2,z2)∈V2,x1＝-x2＝x0,y1＝-y2＝y0>0,z1＝z2＝z0的，因此， 得出Q1∈L2，Q2∈L1的必要条件是： 这表示x0取决于y0，并且z0可以是任何值；在这种情况下，令y0＝y1＝-y2＝1，z1＝z2 ＝z0＝0,便得到x0＝x1＝-x2＝0.0585,然后得到P1(x1,y1,z1)＝P1(0.0585,1,0) ,P2(x2,y2, z2)＝P2(-0 .0585 ,-1 ,0)；因此，开关控制器F(x,y ,z)＝(x0s(y) ,y0s(y) ,z0s(z))T的x0＝ 0.0585,y0＝1,z0＝0,这里s(y)或s(z)是饱和函数，其描述如下： α是饱和函数的斜率； 根据上述理论分析，设计开关控制器s0＝s(y) ,w0＝F(x,y,z)＝(x0s(y) ,y0s(y) , z0s(z))T,x0＝0.0585,y0＝1,z0＝0；从系统(11)中获得 同样，根据系统(6)和(11)，构建以下系统： 其中，参数切换控制器为，F(x,y,z)为平衡点切换控制器；在此，T(x,y,z)和F(x, 11 CN 111582490 A 说　明　书 6/11 页 y,z)是饱和函数系列，如下所示： 式中M为在x,y方向的控制器平衡点个数，决定z方向的涡卷数目；L为在z方向的控 制器平衡点个数，决定z方向的涡卷数目； 表示M项累加； 应用预测器校正器算法求解分数阶微分系统(13)，当αi>0.916,x0＝0.0585,y0＝ 1,z0＝0,M＝5时，得到分数阶12翼混沌吸引子；当x0＝0.0585,y0＝1,z0＝1.125,M＝2,L＝1 时，获得6×4网格多翼混沌吸引子。 本发明的有益效果在于：本发明首先确定分数阶Rucklidge系统的分数阶形式；然 后将分数阶Rucklidge系统在其两个对称平衡点处线性化，以获得两个基本的分数阶线性 系统；接着构造一个异宿环，通过饱和函数切换控制来连接两个基本的分数阶线性系统的 所有平衡点以实现网格多翼混沌吸引子生成器，可以捕获广义的Lorenz吸引子的基本特性 并产生“蝴蝶效应”，由于其构造系统是三个不带乘法器的分数阶微分方程，因此其硬件电 路实现更为简单，并且具有潜在的工程应用。 附图说明 图1为本发明的流程图。 图2为线性分数阶系统的稳定性区域示意图。 图3为αi>0.916时系统的双翼混沌吸引子示意图。 图4为αi＝0.92时系统(13)的12翼混沌吸引子示意图。 图5为αi＝0.93时系统的6×4网格多翼混沌吸引子示意图。