技术摘要：
本发明公开一种基于混合量测的配电网分布式状态估计方法，包括如下步骤：步骤1，首先利用配电网中μPMU和SCADA的量测数据构成混合量测，考虑混合量测背景下的数据结合问题和时间同步问题，并对混合量测进行建模；步骤2，考虑配电网系统节点的电气距离，以模块度为评价  全部
背景技术：
随着电网规模的日渐增大以及可再生能源的积极发展，给电力系统带来更多的不 确定性。同时，为了提高对配电网的实时监控能力，量测技术也不断更新进步，但是，μPMU、 SCADA、AMI等量测具有不同的精度、速度，为了充分利用量测设备提供的量测数据，对多量 测进行混合以提高状态估计的实时性与可靠性势在必行。 电力系统分区是分布式状态估计的重要组成部分，合理分区是保证状态估计计算 精度和降低计算复杂度、提高运算效率的关键前提。通过将节点众多的电力系统分成若干 个高内聚、低耦合的子区域，可以避免计算时矩阵维数太大引入的计算占用空间大、运行时 间长甚至结果难以收敛的情况，大大提高了电力系统状态监测的运算效率。 随着分布式电源电源的大量接入配电网，其出力间歇性、负荷需求差异性、线路参 数不确定性以及量测数据通信延时性等多元未知噪声给传统的集中式状态估计带来巨大 的阻碍，使用分布式状态估计技术对配电网进行态势感知有着重要的意义。 基于以上分析，本案由此产生。
技术实现要素：
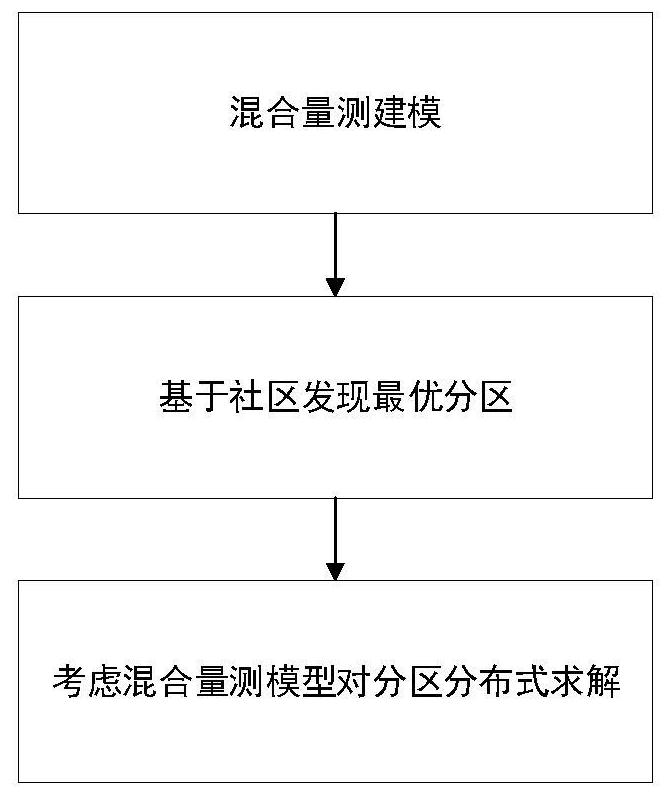
本发明的目的，在于提供一种基于混合量测的配电网分布式状态估计方法，其可 弥补当前状态估计方法在获得量测数据实时性上的不足，提高状态估计算法的精度与速 度，为配电网的安全评估故障定位提供了理论支撑。 为了达成上述目的，本发明的解决方案是： 一种基于混合量测的配电网分布式状态估计方法，包括如下步骤： 步骤1，首先利用配电网中μPMU和SCADA的量测数据构成混合量测，考虑混合量测 背景下的数据结合问题和时间同步问题，并对混合量测进行建模； 步骤2，考虑配电网系统节点的电气距离，以模块度为评价指标，基于社区发现算 法对配电网进行非重叠的最优分区； 步骤3，根据混合量测的模型与最优分区结果，对配电网进行分布式状态估计。 上述步骤1中，配电网的非线性量测方程表示为： z＝h(x) v 其中，z是a×1量测向量，h(x)是a×1非线性量测函数向量，v是a×1误差向量，x为 b×1状态向量，a、b分别是量测量及状态量的个数； 基于加权最小二乘法的状态估计目标函数表示为： 5 CN 111581768 A 说　明　书 2/7 页 其中，J为最小二乘法的目标函数，zi为量测向量z中的第i个元素， 为非线性 量测函数向量h(x)中与状态向量x中第i个元素的估计值 对应的元素，wi为状态向量x中第 i个元素xi的权重。 上述步骤1中，考虑混合量测背景下的数据结合问题，具体包括使用基于等效支路 电流、等效节点电压的量测变换方法，将每个节点的每个象限，视为单个节点单相化处理， 对于一个有n个节点的不平衡配网，所有的节点编号为{1,2,……}，每个节点的相数{m1 , m2,…,mn}，m∈{1,2,3}，构成 导纳矩阵Y。 上述步骤1中，考虑混合量测背景下的时间同步问题，具体内容是： 针对系统在状态估计时间内发生微小的变化，引起的时移误差，确定SCADA采样的 时间断面，并将状态估计周期内的μPMU时间序列和SCADA数据进行整合起来，实现时间兼 容。 首先估计SCADA数据的量测时刻： 其中，ti为估计的第i个SCADA量测时刻，zti为第i个量测数据，K为系数向量，s_f为 状态估计时间内采样的总个数，ξ为误差； SCADA数据的近似时移误差表示为： est＝KΔt＝K(tSE-ts_f) 其中，eSt为近似时移误差，tSE为状态估计断面时刻，ts_f为状态估计之前收到的最 后一个SCADA数据的采样时刻估计值； 由于tSE-ts_f的范围为[0,TSCADA]，TSCADA为SCADA量测的数据上传周期，系数向量K是 根据一组服从正态分布的数据估计得到，因此，eSt近似地服从正态分布； 所以，SCADA的误差vs表示为： vs＝esm est 其中，eSm为SCADA的量测误差； 方差矩阵表示为： 其中，上标T为矩阵的转置，td为tSE-ts_f。 上述状态估计周期内的μPMU时间序列通过AR(p)模型估计出； AR(p)模型的一般数学形式为： zt＝φ0 φ1zt-1 φ2zt-2 … φpzt-p εt 其中，φ0为常数项，φ1 ,… ,φp为模型参数，εt为高斯白噪声均值为0，方差为δ， yt-1,yt-2,…,yt-p为序列中yt的前p个序列。 上述将状态估计周期内的μPMU时间序列和SCADA数据进行整合起来，实现时间兼 容的具体内容是：将μPMU和SCADA混合量测的相角统一，在状态估计过程中，指定给安装μ PMU的某一节点为状态估计的参考节点，以相角量测值作为状态估计的初始值。 上述步骤2中，配电网系统节点的电气距离的计算方法是： 定义两点之间电压灵敏度为两点的电流幅值/电压幅值灵敏度之比，表示为： 6 CN 111581768 A 说　明　书 3/7 页 其中， 为i节点p相对j节点q相的灵敏度， 为j节点q相对i节点p相的灵敏度， 为i节点p相和j节点q相的电压相量， 为注入电流相量的幅值； 基于以上灵敏度，定义i、j节点间电气距离wij为： 其中， 为i节点p相与j节点q相之间的电气距离，a,b,c为节点的三相。 上述步骤2中，以模块度为评价指标，基于社区发现算法对配电网进行非重叠的最 优分区的具体内容是： 步骤2a，定义模块度Q为： 其中，C表示社区，P为配电网系统的社区的集合，ci表示i顶点所属的社区；δ(ci , cj)表示若i、j顶点属于同个社区，则取1，否则为0；ki为顶点的度，表示与点i相连的所有边 的权重之和，m为网络中所有边的权重之和；网络模块度Q看作各个子模块的模块度之和，Q 的取值范围为(-1,1)，当配电网整体划分为一个社区时，Q＝0； 步骤2b，对于有N个顶点的配电网系统，首先将每个顶点初始化为各自独立的社 区，即有N个不同的社区，然后对于每个顶点i，及其所有的相邻顶点j，计算把顶点i从它所 在的社区移动到顶点j所在的社区的模块度增量变化ΔQ，将顶点i移动至ΔQ最大且非负的 相邻顶点j所在的社区，将顶点i从所属的社区c1移动至于j所属的社区c2，形成新的社区c1' 和c2 '；如果所有ΔQ都小于0，则顶点i仍停留在原社区中；此过程按顺序应用于所有的顶 点，并且重复迭代，直到没有顶点移动，即任何一个顶点的移动都不会增大模块度Q； 步骤2c，将模块度Q不再增大时的配电网网络分布的每个社区看作一个顶点，构成 一个新的网络，新顶点之间的边的权重等于原两个社区之间的边的权重之和，新顶点的自 环的权重等于该社区中所有边的权重的两倍，变换后网络的度之和保持不变； 步骤2d，基于步骤2c得到的新的网络，返回步骤2b，重复步骤2b-2c反复迭代，直到 网络不再改变，即模块度已达到最大值。此时的配电网系统被分割为多个高内聚的非重叠 子区域——“社区”，具有对内高耦合性、对外低耦合行特征。 上述步骤3的具体内容是： 步骤31，每个分区的独立状态估计模型表示为： 7 CN 111581768 A 说　明　书 4/7 页 minJ(x)＝[z-h(x)]TW[z-h(x)] 其中，W为混合量测的权重矩阵； 步骤32，对状态估计模型计及各分区的混合量测结果进行分布式求解等价为求解 迭代： 其中，k＝k 1为分布式求解该分区的迭代次数，xk 1为进行k 1次迭代后的状态量， 和 分别表示C1社区及其相邻社区C2第k次迭代的状态量，分布式求解迭代的收敛条件 为达到最大迭代次数或迭代后状态量的变化小于收敛极限。 采用上述方案后，本发明与现有技术相比，具有以下优点： (1)本发明可用于弥补了当前状态估计方法在获得量测数据实时性上的不足，提 高了状态估计算法的精度与速度，为配电网的安全评估故障定位提供了理论支撑； (2)与现有的配电网模型相比，本发明侧重于对配电网三相区间进行建模估计，更 具有工程应用价值，通过边界注入伪量测、将SCADA与μPMU量测混合，提高配电网状态估计 的精度与实时性； (3)本发明中针对配电网最优分区进行分布式状态估计，根据社区发现算法对配 电网进行最优分区，避免了配电网多维不确定性对传统集中式状态估计带来的阻碍，大大 提高了状态估计的效率与精度。 附图说明 图1是本发明配电网混合量测布置示意图； 图2是本发明社区发现算法的分区结果示意图； 图3是本发明分布式状态估计流程图； 图4是本发明的流程图。