技术摘要：
本发明公开了一种基于判别正则化局部保留投影的图像数据降维方法及系统。该方法包括：获取样本图像；将样本图像切割为样本向量，对各样本向量进行L2范数归一化处理，得到处理后的样本向量xi；确定第一相似性矩阵Sij；根据确定第二相似性矩阵S'ij，其中，W为投影矩阵，Bij  全部
背景技术：
图像的数据降维是将高维数据投影到低维空间，同时尽可能多地保持原始数据的 内在信息，从而使得高维数据能够表示在低维空间中。通过这种操作可以减少原有数据的 冗余性，提高对数据处理的效率和针对性。线性数据降维最典型的降维方法包括：主成分析 (Principal  component  analysis，PCA)和线性判别分析(Linear  discriminant  analysis，LDA)。这两种方法理论成熟，计算简单、计算速度快，但是这些方法都属于线性维 数约简方法，无法提取数据的非线性结构特征。为了解决这个问题，最直观的思路是基于核 对线性模型进行非线性扩展，但是基于核的方法计算负担大，而且无法提取数据的局部结 构特征。 基于流形学习的非线性方法为图像数据降维提供了一条解决途径，流形学习是以 非监督方式操作的一大类非线性降维方法。但传统的基于流形学习的非线性维数约简方法 都存在out-of-sample问题，目前有两类典型的学习方法能解决这个问题，一类是基于相似 性保留的线性化流形学习方法，典型算法如：邻域保持嵌入(Neighborhoods  preserving  embedding，NPE)和局部保留投影(Locality  preserving  projections，LPP)此类算法通过 线性嵌入来保留数据的流形结构特征：另一类是基于回归的流形结构保留算法，如SEANC、 RCFE和SEC，这类算法通过线性回归的方式来近似数据的非线性流形结构，从而保留数据的 流形结构。 在流形学习中，首先需要采用图来描述数据的本质结构，图的优劣决定着流形学 习方法能否有效提取数据的本质结构特征。 CGE利用类柯西分布强调对流形的局部性和拓扑关系保留能力。但是CGE为了保留 数据的拓扑关系，过度强调局部结构特征，这容易造成流形结构，特别是分布稀疏的区域， 在嵌入空间中断裂成多个局部领域。这种嵌入模型对于多流形数据容易造成不同流形在嵌 入空间中的交叠，不利于提取不同流形之间的判别信息。 L1-norm和L2,p-norm的LPP，这些方法都可以等价看作为L2-norm意义下，根据样本 在嵌入空间中分布特征的不同，对相似度重新加权的过程。但是这些方法只强调相似性。对 局部稠密分布的流形结构，容易过多引入非局部信息，从而破坏流形数据的局部拓扑关系。 LSPP，DSPGE利用了稀疏描述对样本的自然判别信息，和对噪声的鲁棒性，这两个 特征，结合LPP建立了鲁棒LPP嵌入模型。这两种方法在嵌入过程中，除了考虑样本点之间的 局部性，而且考虑了样本之间的稀疏重建关系，有效提高了对数据局部本质结构特征的提 取能力。但是稀疏表示的尺度无关系，使得这些方法对不同区域分布特征的差异性考虑不 足。 5 CN 111553417 A 说　明　书 2/9 页
技术实现要素：
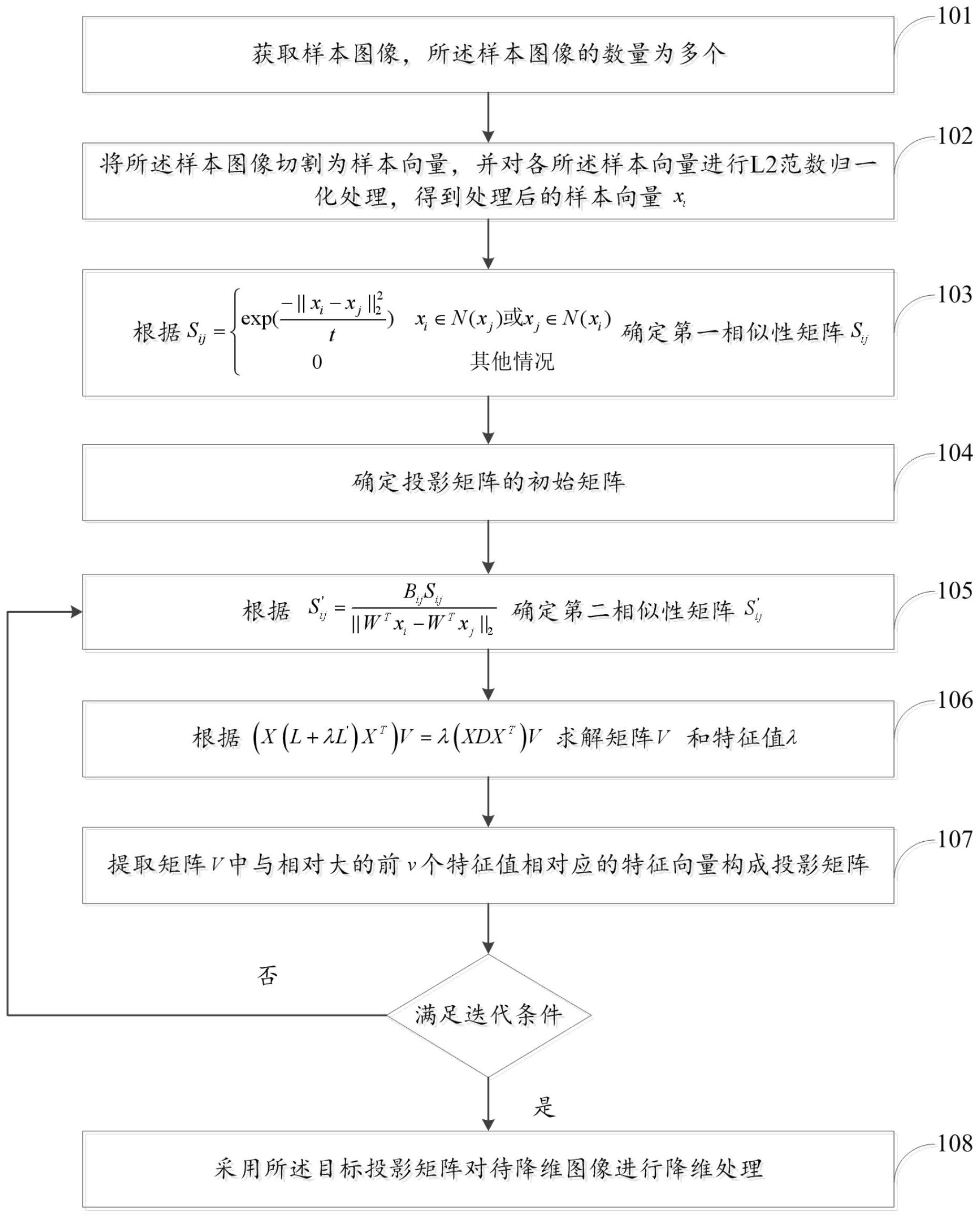
本发明的目的是提供一种基于判别正则化局部保留投影的图像数据降维方法及 系统，同时考虑了数据的相似性和差异性。 为实现上述目的，本发明提供了如下方案： 一种基于判别正则化局部保留投影的图像数据降维方法，包括： 获取样本图像，所述样本图像的数量为多个； 将所述样本图像切割为样本向量，并对各所述样本向量进行L2范数归一化处理， 得到处理后的样本向量xi，i＝1,2,…n，n为样本图像的数量； 根据 确定第一相似性矩阵Sij，其中 t是一个热核参数且t≥0,||·||2是L2范数符号，N(xi)表示距离xi最近k个样本集合； 确定投影矩阵的初始矩阵，所述投影矩阵为正交的d×v矩阵，v为投影后的维度，d 为样本向量的维度； 根据 确定第二相似性矩阵S′ij，其中，W为投影矩阵，Bij为弹 性矩阵，Bij＝sign(Sij-s)，s为第一相似性矩阵中大于0的元素的平均值； 根据(X(L λL')XT)V＝λ(XDXT)V求解矩阵V和特征值λ，其中，L＝D-S，L'＝D'-S',D 和D'均为对角矩阵， X＝[x1,x2,...,xn]； 提取矩阵V中与相对大的前v个特征值相对应的特征向量构成投影矩阵； 跳转至“根据 确定第二相似矩阵S′ij”步骤，直至满足迭代条 件，将最后得到的投影矩阵记为目标投影矩阵； 采用所述目标投影矩阵对待降维图像进行降维处理。 可选的，所述采用所述目标投影矩阵对待降维图像进行降维处理，具体包括： 获取待降维图像； 将所述待降维图像切割为样本向量x； 根据Y＝W'Tx对所述待降维图像进行降维，其中，W'为目标投影矩阵，Y为所述待降 维图像降维后的数据。 可选的，所述迭代条件为迭代次数达到设定次数。 可选的，所述迭代条件为相邻两次迭代得到的目标值J的差值ΔJ小于设定阈值， 其中，目标值 其中，L TP＝X(L λL')X 。 可选的，所述方法还包括： 获取测试样本图像； 将所述测试样本图像切割为测试样本向量； 采用所述目标投影矩阵对所述测试样本向量进行降维； 6 CN 111553417 A 说　明　书 3/9 页 采用分类器对降维后的测试样本向量进行识别； 用于根据识别结果评估所述投影矩阵的优劣。 本发明还提供了一种基于判别正则化局部保留投影的图像数据降维系统，包括： 图像获取模块，用于获取样本图像，所述样本图像的数量为多个； 图像切割模块，用于将所述样本图像切割为样本向量，并对各所述样本向量进行 L2范数归一化处理，得到处理后的样本向量xi，i＝1,2,…n，n为样本图像的数量； 第一相似性矩阵确定模块，用于根据 确定第一相似性矩阵Sij，其中t是一个热核参数且t≥0,||·||2是L2范数符号，N(xi)表示 距离xi最近k个样本集合； 初始投影矩阵确定模块，用于确定投影矩阵的初始矩阵，所述投影矩阵为正交的d ×v矩阵，v为投影后的维度，d为样本向量的维度； 第二相似性矩阵确定模块，用于根据 确定第二相似性矩阵 S′ij，其中，W为投影矩阵，Bij为弹性矩阵，Bij＝sign(Sij-s)，s为第一相似性矩阵中大于0的 元素的平均值； 特征求解模块，用于根据(X(L λL')XT)V＝λ(XDXT)V求解矩阵V和特征值λ，其中，L ＝D-S，L'＝D'-S',D和D'均为对角矩阵， X＝[x1,x2,...,xn]； 投影矩阵确定模块，用于提取矩阵V中与相对大的前v个特征值相对应的特征向量 构成投影矩阵； 降维处理模块，用于采用所述目标投影矩阵对待降维图像进行降维处理。 可选的，所述图像获取模块，还用于获取待降维图像；图像切割模块，还用于将所 述待降维图像切割为样本向量x；降维处理模块，还用于根据Y＝W'Tx对所述待降维图像进行 降维，其中，W'为目标投影矩阵，Y为所述待降维图像降维后的数据。 可选的，所述迭代条件为迭代次数达到设定次数。 可选的，所述迭代条件为相邻两次迭代得到的目标值J的差值ΔJ小于设定阈值， 其中，目标值 其中，LP＝X(L λL')XT。 可选的，所述图像获取模块还用于获取测试样本图像；图像切割模块还用于将所 述测试样本图像切割为测试样本向量；所述降维处理模块还用于采用所述目标投影矩阵对 所述测试样本向量进行降维； 所述系统还包括： 分类识别模块，用于采用分类器对降维后的测试样本向量进行识别； 准确性确定模块，用于根据识别结果评估所述投影矩阵的优劣。 根据本发明提供的具体实施例，本发明公开了以下技术效果：本发明提供的判别 正则化局部保留投影的图像数据降维方法及系统，建立了一个基于L2,1范数的局部判别投 7 CN 111553417 A 说　明　书 4/9 页 影来学习数据的局部拓扑结构，并将局部判别投影作为LPP的正则项与LPP组成弹性距离， 使局部领域的大小能够根据分布特征自适应调整，对于分布稠密的区域，能够防止过多非 局部信息的引入，避免造成流形结构在嵌入过程中的扭曲和对局部拓扑关系的破坏，同时 能够很好地保持局部样本分布的多样性和差异性，更好地描述数据的局部本质结构特征。 附图说明 为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所 需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施 例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获 得其他的附图。 图1为本发明实施例1提供的基于判别正则化局部保留投影的图像数据降维方法 流程示意图； 图2为本发明实施例1中Coil20数据集识别准确率与投影维度变化曲线图； 图3为本发明实施例1中Yale数据集识别准确率与投影维度变化曲线图； 图4为本发明实施例1中ORL数据集识别准确率与投影维度变化曲线图； 图5为本发明实施例2提供的基于判别正则化局部保留投影的图像数据降维系统 结构图。