技术摘要：
本发明公开基于粒子群优化算法和均匀设计采样结合Nataf变换的数据处理方法及数据处理系统，包括以下步骤：S1：对电力系统进行数据识别，得到基础数据，所述的基础数据包括输入随机变量X＝[x1,x2,...,xi,...xm]T的概率分布特性及其相关系数矩阵ρX；定义n为采样规模，定  全部
背景技术：
电力系统中本来就有很多的随机因素，随着新能源电力系统的发展，大规模风力 和光伏发电并网，使电力系统中的不确定性急剧增加。研究表明电力系统中的随机性因素 大都满足某一的概率分布特性(例如：风电场风速大致服从双参数的Weibull分布、电力负 荷大都服从正态分布、光伏电站的有功出力近似服从Beta分布等)及具有相关性。为了更简 单有效的分析电力系统中随机关联性因素对电力系统运行的影响，在已知风速、光照强度、 电力负荷等随机变量分布特性的条件下，简单高效可处理随机变量相关性的概率潮流 (Probabilistic  Load  Flow，PLF)计算方法对分析电网运行有着重要意义。
技术实现要素：
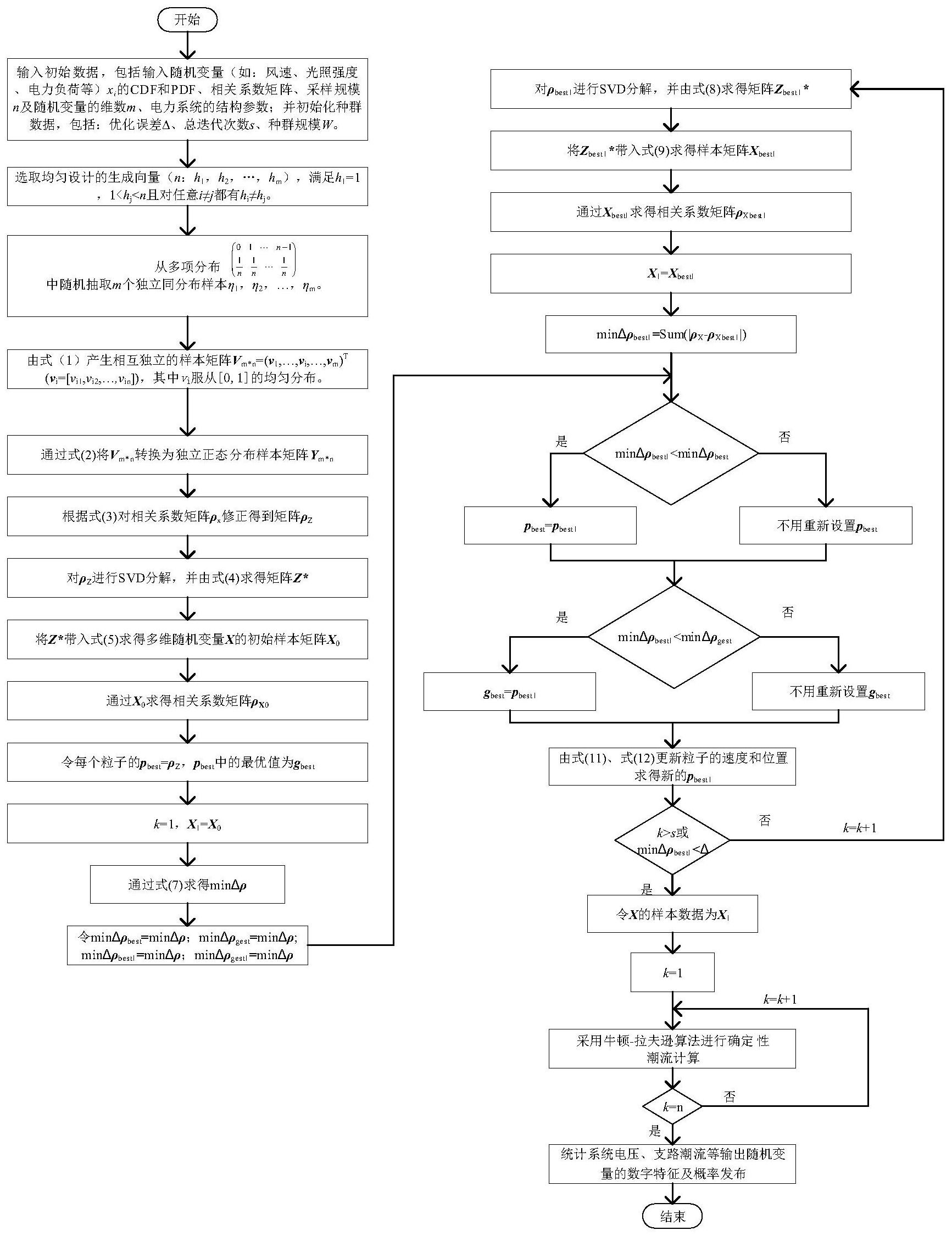
为克服上述现有技术与方法的不足，本发明提出了基于粒子群优化算法和均匀设 计采样结合Nataf变换的数据处理方法及数据处理系统。本发明有如下优点：1)不需要复杂 的变换，实现简单；2)不受不同边缘分布的影响，适应面广；3)能处理随机变量相关系数矩 阵正定和非正定的情形；4)能较好地适应未来电力系统随机波动性强的特点，具有较好的 工程应用前景。 为解决上述技术问题，本发明的技术方案如下： 基于粒子群优化算法和均匀设计采样结合Nataf变换的数据处理方法，包括以下 步骤： S1：对电力系统进行数据识别，得到基础数据(即采样数据)，所述的基础数据包括 输入随机变量X＝[x1,x2,...,xi,...x Tm] 的概率分布特性及其相关系数矩阵ρX；定义n为采 样规模，定义m为输入随机变量的维数；定义s为迭代次数；定义Fxi( )为xi的累积分布函数； 为 的反函数； S2：根据基础数据，通过均匀采样算法，得到第一优化数据； S3：根据第一优化数据，通过奇异值分解和Nataf变换(边缘变换技术)进行优化， 得到第二优化数据； S4：根据第二优化数据，通过粒子群优化算法进行优化，得到第三优化数据； S5：根据第三优化数据通过潮流计算，得到节点电压D、支路潮流E的数字特征及对 应的概率分布。 本发明中有如下优点：1)不需要复杂的变换，实现简单；2)不受不同边缘分布的影 响，适应面广；3)能处理随机变量相关系数矩阵正定和非正定的情形；4)能较好地适应未来 电力系统随机波动性强的特点，具有较好的工程应用前景。 6 CN 111552918 A 说　明　书 2/8 页 在一种优选的方案中，所述的S2包括以下子步骤： S2.1：根据基础数据，随机定义生成向量n：h1，h2，…，hm；且满足h1＝1，1