技术摘要：
本发明披露了一种重优化深度自动编码器，其特征在于：包括第一经典深度自动编码器模块、K‑Means聚类模型模块和第二经典深度自动编码器模块；所述第一经典深度自动编码器模块训练完成后，通过所述第一经典深度自动编码器模块获得一重构误差集；所述K‑Means聚类模型模  全部
背景技术：
深度自编码器(Deep  Auto  Encoder，AE)是一种学习输入数据的表示(编码)的一 种人工神经网络，通常作为一种特征提取的方法被我们使用。从结构上说，自编码器是一种 前馈神经网络，它包含一个输入层，一个隐层以及一个输出层。其中的输出层所包含的神经 元个数与输入层的神经元个数相同，这样便可以对输入进行重构。 当前普遍使用的监督型异常检测系统具有优秀的异常检测性能归功于其能从大 量的带标签样本中学习到丰富的特征表示的能力。在充足的有标签数据下，这些方法往往 可以取得比较好的异常检测性能。然而，一旦数据无标签，这些方法就会失效。尤其地，航空 发动机监控数据属于极端类不平衡数据，在实际飞行过程中获取的监控数据中正常数据远 远大于异常数据，航发的异常数据较少甚至完全没有异常数据；其次，给监控数据打标签一 般由专家手动完成，使得在航空发动机实际运行过程中获取准确的有代表性的异常标签数 据非常困难。此外，从有限的机队中难以获取包含所有可能的异常行为的异常数据。这些问 题导致监督型异常检系统在航空发动机实际异常检测领域的应用非常受限。 而无监督型异常监测系统中，最大的优势是能在无数据标签条件下实现异常检 测，适应于标签数据难以获取的场景。因此，无监督型异常检测方法在航空发动机异常检测 领域具有更好的研究价值和发展前景。同时，航空发动机在实际运维中积累了大量的监控 性能数据，这些性能数据可为建立无监督型异常检测方法提供基础。 与正常样本相比，异常样本的差异主要表现在低维特征空间的特征存在偏差以及 异常样本更难重构。鉴于此，本文提出了一种新的无监督深度学习方法一重优化深度自编 码器(Re-optimized  Deep  Auto-Encoder，R-DAE)用于提升无数据标签下，尤其是燃气轮机 等异常检测性能。R-DAE将降维后的低维特征和引起的重构误差一起作为输入样本的低维 表示，可以有效地解决维数灾乱问题并且还包含更多有用信息，更有利于后续的异常检测。 同时，当传统DAE无法提取输入样本的有效特征时，R-DAE可以通过重构误差反映样本的差 异。
技术实现要素：
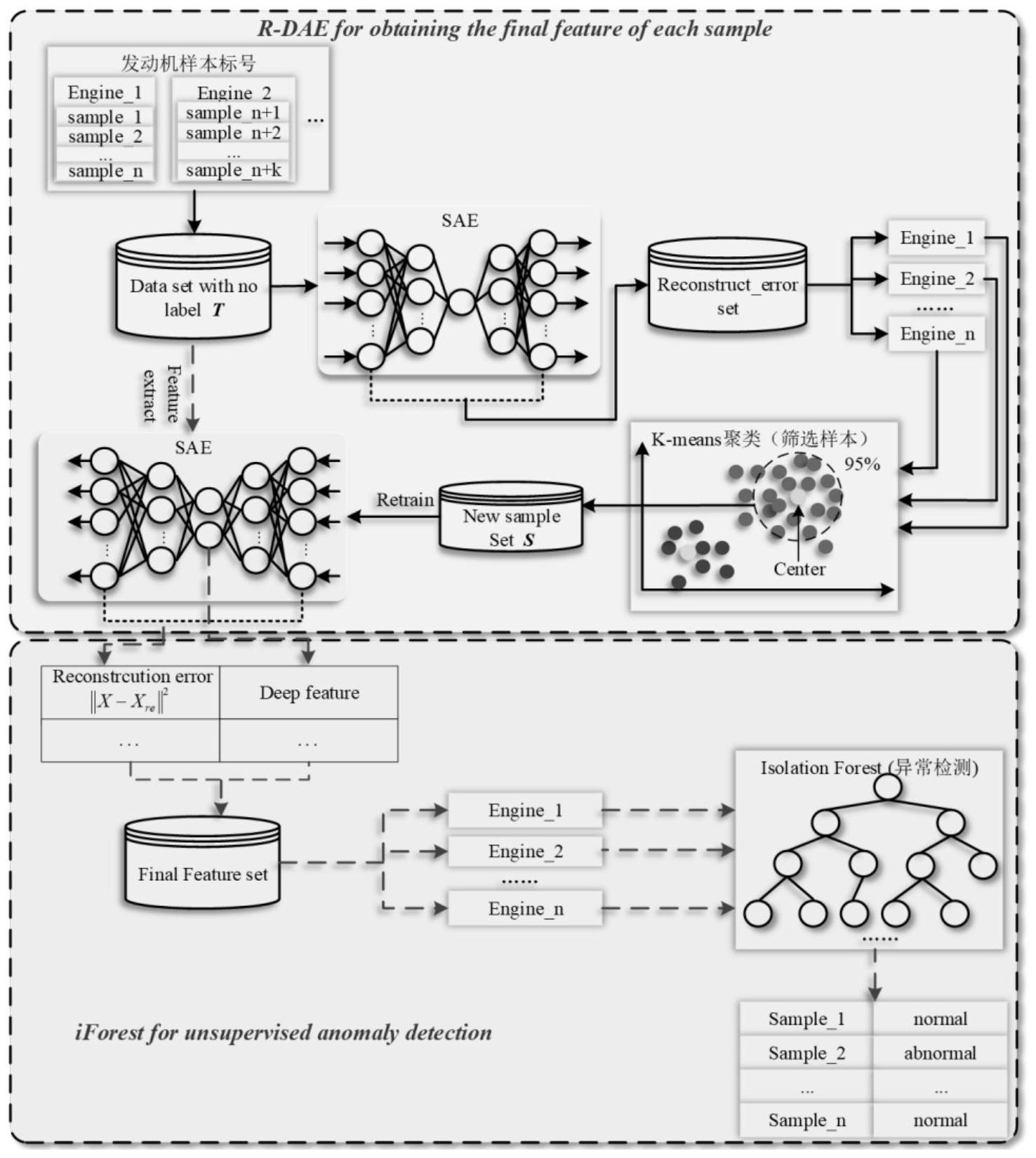
本发明提出了一种重优化深度自动编码器，其特征在于： 包括第一经典深度自动编码器模块、K-Means聚类模型模块和第二经典深度自动 编码器模块； 所述第一经典深度自动编码器模块训练完成后，通过所述第一经典深度自动编码 器模块获得一重构误差集； 所述K-Means聚类模型模块对所述重构误差集进行聚类，剔除其中重构误差较大 4 CN 111598222 A 说　明　书 2/12 页 的异常样本，保留正常样本作为新训练集； 用所述新训练集对所述第二经典深度自动编码器模块进行训练。 如上所述的重优化深度自动编码器，其特征在于： 采用原始无标签数据集对所述第一经典深度自动编码器模块进行训练。 如上所述的重优化深度自动编码器，其特征在于： 所述重构误差集E由欧式距离ED来定义和构成： EDj＝(xj-y 2j) ， 其中，xj是所述原始无标签数据集中的第j个数据；yj是训练完成后的所述第一经 典深度自动编码器模块对所述原始无标签数据集进行编码、解码后的输出数据集中的第j 个数据，EDj是所述第一经典深度自动编码器模块重构误差集中的第j个数据； E＝{ED1，ED2，......EDn}，E是所述第一经典深度自动编码器模块的重构误差集； J为1-n之间的整数。 如上所述的重优化深度自动编码器，其特征在于： 所述K-Means聚类模型模块对所述重构误差集进行聚类时，保留距离所述K-Means 聚类模型模块的聚类中心最近的s个样本作为所述正常样本来构成所述新训练集； 其中s为事先设定的1-n之间的整数。 如上所述的重优化深度自动编码器，其特征在于： s/n＝95％。 如上任一所述的重优化深度自动编码器，其特征在于： 所述第一经典深度自动编码器模块、第二经典深度自动编码器模块均是多个自动 编码器通过级联堆叠的方式来构成的。 如上所述的重优化深度自动编码器，其特征在于： 每个自动编码器包括一个输入层和一个隐藏层，通过级联堆叠的多个自动编码器 中，前一个自动编码器的隐藏层作为下一个所述自动编码器的输入层； 最后一个自动编码器的隐藏层作为输出层输出数据的深度特征。 如上所述的重优化深度自动编码器，其特征在于： 所述第一经典深度自动编码器模块、第二经典深度自动编码器模块还包括多个级 联堆叠的解码器，每个解码器包括一个作为输入层的隐藏层和一个输出层； 所述最后一个自动编码器的隐藏层作为级联堆叠的解码器的第一个输入层，每个 解码器的输出层作为下一个解码器的输入层； 所述级联堆叠的解码器和所述级联堆叠的编码器对称设置。 如上所述的重优化深度自动编码器，其特征在于： 所述编码器将输入向量x经过编码函数fθ映射到隐藏层h的过程执行如下算法： 其中x∈Rn表示原始输入向量，h∈Rm表示隐藏层向量，z∈Rn表示输出层向量； W是m×n权重矩阵，b是偏置向量， 表示隐层向量，S(·)为节点激活函数； 所述解码器将隐藏层h经过非线性映射函数gθ′重构输入的过程执行如下算法： z＝gθ′(h)＝S(W′*h b′) 5 CN 111598222 A 说　明　书 3/12 页 其中W′是n×m维的权重矩阵， 是偏置向量， 表示输出层向量。 如上所述的重优化深度自动编码器，其特征在于： 所述第一经典深度自动编码器模块、第二经典深度自动编码器模块的训练按照如 下原则优化： 利用反向传播算法寻找最优参数{θ，θ′}＝{W，b；W′，b′}，使得由下述方程定义的 所述输出层向量z与所述原始输入向量x之间的均方误差LH(x，z)最小： LH(x，z)＝||x-z||2        ＝||x-gθ(fθ(x))||2。 如上所述的重优化深度自动编码器，其特征在于： 使用mini-batch梯度方法来寻找所述均方误差LH(x，z)最小化的所述最优参数 {θ，θ′}＝{W，b；W′，b′}。 如上所述的重优化深度自动编码器，其特征在于： 所述mini-batch梯度方法包括将作为输入向量的训练集划分为若干个mini- batch，每次将一个mini-batch输入到深度自动编码器块中，以整个mini-batch的均方误差 的平均值作为损失函数，如下述方程所示： 式中，K表示mini-batch的大小，求解所述均方误差LH(x，z)最小值即可获得所述 最优参数{θ，θ′}＝{W，b；W′，b′}。 基于本发明所提出的重优化深度自编码器，当传统DAE无法提取输入样本的有效 特征时，R-DAE可以通过重构误差反映样本的差异。 本发明还提出了一种发动机自动检测系统，所述检测系统包括如上任一所述的重 优化深度自编码器和一个孤立森林检测模块，其特征在于： 将每台发动机的特征集和重构误差集作为该发动机的最终特征集FF，并输入到所 述孤立森林检测模块中进行异常检测。 如上所述的检测系统，其特征在于： 所述第一经典深度自动编码器模块通过如下方式构建的训练集进行训练； 一、利用滑动窗口的方法构造每台发动机的样本集，并按时间顺序对每台发动机 的样本集进行标记，标记完成的所有发动机的样本集会被组合成最终的原始无标签样本集  T， Ti＝{ti1，ti2，...，tir} T＝{T1，T2，....，Tn} 其中，Ti表示第i台发动机的样本集；tir表示第i台发动机的第r个样本。 二、利用样本集T对所述第一经典深度自动编码器模块进行训练，并用训练完成的 所述第一经典深度自动编码器模块计算样本集T的重构误差集E， 6 CN 111598222 A 说　明　书 4/12 页 Ei＝{ei1，ei2，...，eir} E＝{E1，E2，....，En} 其中Ei＝{ei1，ei2，...，eir}表示第i台发动机样本集Ti所对应的重构误差集，eir表 示第i台发动机的第r个样本对应的重构误差， 表示原始无标签样本集、 表示经所述第 一经典深度自动编码器模块处理后的样本集； 表示欧式距离的平方。 如上所述的检测系统，其特征在于： 利用K-means聚类方法分别将每台发动机的重构误差集E进行聚类，以筛选出正常 样本集S； 用所述正常样本集S来训练所述第二经典深度自动编码器模块，即获得训练完成 的所述重优化深度自编码器。 如上所述的检测系统，其特征在于： 用所述重优化深度自编码器对发动机的所述原始无标签样本集T进行处理，分别 获得所述原始无标签样本集T的特征集F， F＝{F1，F2，....，Fn} 和重构误差集RE， RE＝{RE1，RE2，....，REn} 其中，Fi＝{fi1，fi2，...，fir}，REi＝{rei1，rei2，...，reir}分别表示第i台发动机样 本集Ti所对应的特征集和重构误差集； 然后用所述原始无标签样本集T对应的所述特征集F和所述重构误差集RE来构建 所述最终特征集FF， FFi＝{[fi1，rei1]，[fi2，rei2]，...，[fir，reir]}。 如上任一所述的检测系统，其特征在于： 采用异常概率A和虚警率F来表示最终的检测结果； 其中异常概率A表示n次检测中该台发动机被检测为异常的概率，由下式定义： 式中，yi表示某台发动机第i次检测的结果，若默认的异常样本被检测出来，则  yi ＝1，否则yi＝0； 虚警率F表示每台发动机中正常样本被检测为异常样本的概率，由下式定义： ri表示某台发动机第i次检测中假异常样本的个数；m表示该台发动机包含样本的 数量，c表示正确的异常样本的个数。 如上所述的检测系统，其特征在于： 用下式方程定义的总体检测精度prep来表示被测出异常的发动机的正确率 7 CN 111598222 A 说　明　书 5/12 页 R表示异常发动机被正确的检测出的数量，N表示样本发动机的台数。 附图说明 图1重优化深度自编码器中AE单元的结构示意图 图2重优化深度自编码器中DAE模块的结构示意图 图3重优化深度自编码器(R-DAE)结构示意图 图4利用R-DAE对航空发动机进行无监督异常检测过程框图 图5滑动窗口提取样本过程 图6发动机拆发前300个飞行循环DEGT变化图 图7样本重构误差示例，a、b、c、d分别表示1、2、3、4号发动机所有样本的重构误差 图8不同样本的重构精度示例，a、b分别表示样本A、B的重构精度 图9四组实验各种方法的虚警率，1第一组对比实验三种方法的虚警率；2第二组对 比实验中两种方法的虚警率；3第三组对比实验三种方法的虚警率；4本文提出方法的虚警 率 图10  RDAE-iForest方法的检测结果 具体实施方法 如图1所示，R-DAE中的AE单元结构示意图，从基本结构上讲，由输入层、隐藏层、输 出层构成，其中输入层的编码器接收输入向量，并将输入向量经编码函数映射到隐藏层，构 成隐藏层向量，隐藏层向量包含输入向量的较深层次特征，譬如边界、轮廓、奇点等。由输入 层、隐藏层构成一个完整的编码过程。 隐藏层向量经输出层解码，构成输出层向量，输出层向量即为输入向量的重构向 量。理想状况下，输出层向量应该能完整重构输入层向量，即二者是一致的，然而，事实上， 完全的重构是不可能实现的，总会或多或少的损失一些特征，这种损失一般用输入、输出向 量的均方误差(Mean  Square  Error，MSE)表示。 从输入层、经隐藏层再到输出层，整个过程的数学描述如下： 若用x∈Rn表示原始输入向量，h∈Rm表示隐藏层向量，z∈Rn表示输出层向量，编 码、解码及训练优化的数学方程如下。 (1)编码过程：将输入向量x经过编码函数fθ映射到隐藏层h的过程，如式(1)所示： 其中W是m×n权重矩阵，b是偏置向量， 表示隐层向量。S(·)为节点激活函 数，本发明选用ReLU函数作为节点激活函数S(·)。 (2)解码过程：将隐藏层h经过非线性映射函数gθ′重构输入的过程，如式(2)所示： z＝gθ′(h)＝S(W′*h b′)   (2) 其中W′是n×m维的权重矩阵， 是偏置向量， 表示输出层向量。 (3)寻找最优参数过程：利用反向传播算法寻找最优参数{θ，θ′}＝{W，b；W′，b′}， 使输出向量z与输入向量x之间的均方误差(Mean  Square  Error，MSE)最小，用式(3)所示的 损失函数表征： LH(x，z)＝||x-z||2 8 CN 111598222 A 说　明　书 6/12 页        ＝||x-gθ(fθ(x))||2   (3) 如图2所示的深度自动编码器(Deep  Auto  Encoder，DAE)，由多个AE级联叠加而 成，即堆叠自动编码器，而叠加的目的，则是提取输入数据更深层的特征，也就说，DAE 网络 试图以更具有代表性的特征去描述原始数据而尽量不损失数据有效信息。DAE的输入-输出 可以用下式来表征： 其中x表示原始输入向量，hi表示n级AE叠加形成的DAE各级隐藏层向量，i为1-  n 之间的整数，表征第i个AE。与单个AE单元相比，DAE的核心就是通过堆叠多个AE的方式，挖 掘原始输入向量x中的深度特征，最后一个AE的隐藏层hn被认为是输入向量x  在低维度上 的最终表示，视为输入向量x的深度特征。也就是说，只需要存储、传输hn，再通过相应的解 码器，得到的输出向量z，即是最接近原始输入向量x的。 如方程3所示，AE的训练优化最终是收敛于输入向量x与经解码器还原后的输出向 量z之间的均方误差最小。故而，尽管实际使用中我们最感兴趣的还是经AE编码后的隐藏层 向量h(因为h在低阶维度上表征了输入向量x的关键特征，同时又尽量没有损失输入向量x 的关键信息)，然而，为了便于训练优化AE，一般会加上解码器，以便将隐藏层向量h还原为 输出向量z。 如图2所示的DAE中，多个级联对接的AE，同时对称的级联堆叠了多个解码器，以便 对最后的隐藏层向量hn予以解码还原为z，从而能够通过对方程3定义的损失函数求最小 值，以获得最优DAE参数{θ，θ′}＝{W，b；W′，b′}。 另外，对于DAE的训练优化，我们采用了mini-batch梯度方法来寻找最优参数。具 体地，将训练集划分为若干个mini-batch，每次将一个mini-batch输入到模型中，以整个  mini-batch的均方误差的平均值作为损失函数，如方程式(4)所示 式中，K表示mini-batch的大小。求解方程式4的最小值，即完成了DAE的训练优化。 图3所示为本发明提出的R-DAE的结构图，由两个经典DAE和一个K-Means聚类模型 组成。其中第一个DAE和K-Means模型组成样本筛选器对输入样本进行筛选，而第二个DAE首 先被筛选后的样本集进行训练，然后用以计算原始样本集中所有样本的重构误差和深度特 征，具体过程如下： 第一，利用原始无标签数据集按照上述方式训练第一个DAE，训练后的DAE用以计 算原始数据集的重构误差集。重构误差集由方程式(5)定义； 第二，得到重构误差集之后，利用K-means聚类模型将其聚为两类。重构误差较大 的一类所对应的样本被认为是异常的，将会被剔除，而另一类所对应的样本暂时被认为是 正常样本。然而，仅通过重构误差不能完全清楚的划分样本。为了使获得的正常样本根据有 代表性，选取离该类聚类中心最近的m个样本作为新的训练集。 9 CN 111598222 A 说　明　书 7/12 页 第三，利用第二步中得到的新训练集训练第二个DAE模型。与原始训练集相比，新 的训练集包含较少的异常样本，甚至没有异常。因此，可以认为第二个DAE只通过正常优化， 这就是所谓的R-DAE，并用以计算原始无标签数据集的重构误差和深度特征，得到样本的最 终特征。 相比于经典的DAE系统，R-DAE编码器系统的有效之处就在于：首先，R-DAE将输入 样本的关键信息保存在一个低维空间中，该低维空间包含了提取的高阶特征和诱导重建误 差的特征。因此，当传统的DAE不能提取输入样本的有效特征时，R-DAE可以通过重构误差来 描述样本间的差异。其次，R-DAE并没有将所有数据的重构误差最小化，只是将正常样本的 重构误差最小化，这使得正常样本的重构误差更小，而异常样本的重构误差则没有。通过R- DAE系统，将正常样本常规处理；而异常样本，由于未经事先的优化训练，通过R-DAE系统时， 会有一定程度的放大，异常会非常容易的被识别出来。 而DAE训练优化中，唯一的标准就是重构误差更小，而不管原始输入样本中是否包 含特定的异常数据，这些异常数据很可能就是现实世界中出现问题的征兆，譬如燃气轮机、 航空发动机等运行的异常数据。如果只是基于传统的DAE来监测真实世界中的燃气轮机、航 空发动机等的运行，反应真实运行状态的异常数据，很可能在初级AE编码中就被剔除掉了， 或者削弱了这种异常，最终不能被识别出来。 我们在R-DAE系统中选用欧式距离(Euclidean  Distance，ED)来表示重构样本与 原始样本的重构误差，具体如公式(5)所示。 ED越小，表示重构样本与原始样本之间的差异越小。在实验过程中，为了便于计 算，本文利用ED的平方代替ED。