技术摘要：
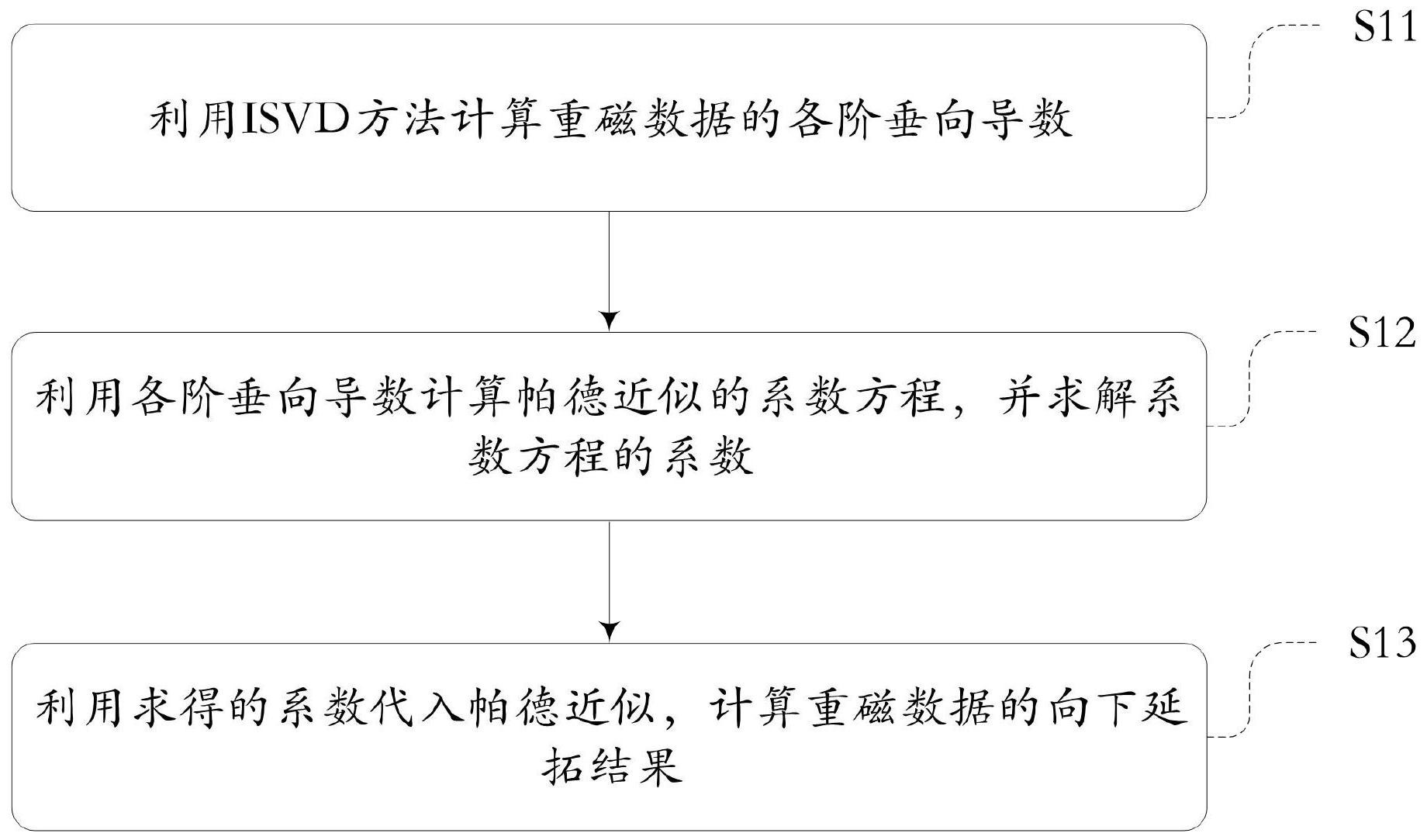
本发明提供了一种基于帕德近似的重磁数据向下延拓方法。该方法包括：利用ISVD方法计算重磁数据的各阶垂向导数；利用各阶垂向导数计算帕德近似的系数方程，并求解系数方程的系数；利用求得的系数代入帕德近似，计算重磁数据的向下延拓结果。本发明提供的这种基于帕德近  全部
背景技术：
向下延拓是卫星、航空重磁数据处理中的经典和关键技术。重磁数据向下延拓可 以增强数据信息，识别弱异常和叠加异常，这对近地表地球物理勘探中从强干扰中提取弱 信息非常重要。泰勒级数展开法是一种简单快速的重磁数据向下延拓方法。泰勒级数展开 法可以一定程度改善向下延拓的不稳定性问题，但是向下延拓的准确性也有待提高。 重磁场向下延拓的泰勒级数展开式可以表示为(Evjen，1936) 其中，u(x,y,z0)为z0高度的重磁场，h(h＞0)是向下延拓的高度，利用公式  (1)进 行向下延拓的关键在于计算重磁场的不同阶垂向导数。Evjen(1936)  利用拉普拉斯方程计 算计算高阶垂向导数，拉普拉斯方程如下： 计算重磁数据高阶垂向导数方法 但他利用的一阶垂向导数是用图解法计算出来的，其计算不便于现代形式的数字 数据且所计算结果精度低。 自快速傅里叶变换(FFT)算法定义以来(Dean，1958；Cooley&Tukey，  1965)，Gunn (1975)实现了使用傅立叶变换来执行垂直导数。Blakely  (1996)给出了波数域中重磁数据 的垂直导数计算的滤波器响应的二维表达式， 其中，F和F-1是傅里叶正反变换对，n是垂向导数的阶数。然而，由于波数域中高频 部分的急剧放大作用，FFT方法中所使用的数据需要很好的去燥和平滑滤波，且由FFT方法 计算的垂向导数也不稳定，这限制了重磁数据向下延拓的深度不超过2个数据点间隔。 Fedi和Florio(2001、2002)提出了一种计算垂直导数的积分二次垂向导数方法 (ISVD方法)，该方法结果比FFT方法更稳定。为了计算重磁数据的一阶垂直导数，他们首先 用波数域对重磁数据进行积分，得到重磁场的标量位 4 CN 111580174 A 说　明　书 2/11 页 其次，根据拉普拉斯方程(3)，他们通过积分函数的二阶水平导数之和(通过有限 差分计算)计算积分函数的二阶垂直导数。至于二阶水平导数，它们的计算可以在空间域中 使用有限差分关系(例如Cordell和Grauch，1985；  Trompat和等人，2003)以精确和稳定的 方式完成，有限差分表达式 最后，他们重复第二步计算重磁数据的高阶垂向导数。利用ISVD法计算重磁数据 的垂向导数时，采用了平滑滤波(垂直积分滤波)和有限差分法相结合的方法，比FFT法稳定 得多。这种方法的优点是使重磁数据向下延拓的稳定性大大提高，但是向下延拓结果的精 度仍然有待于提高。 基于泰勒级数展开，利用ISVD计算垂向导数的向下延拓称为  ISVD-Taylor向下延 拓方法，上述方法提高了向下延拓的稳定性。然而，泰勒级数展开式不是数学逼近理论中最 精确的近似(Ma  et  al，2002)。帕德近似(本文翻译自Padé  approximation)对函数的逼近 比Taylor级数展开的精度高，误差小(Zhang等人，2016)。
技术实现要素：
本发明要解决的技术问题是提供一种基于帕德近似的重磁数据向下延拓方法及 装置，能够提供稳定且准确的重磁数据向下延拓。 为解决上述技术问题，本发明提供了一种基于帕德近似的重磁数据向下延拓方 法，所述方法包括：利用ISVD方法计算重磁数据的各阶垂向导数；利用各阶垂向导数计算帕 德近似的系数方程，并求解系数方程的系数；利用求得的系数代入帕德近似，计算重磁数据 的向下延拓结果。 在一些实施方式中，利用ISVD方法计算重磁数据的各阶垂向导数，包括：利用波数 域的重磁数据换算方法计算重磁数据的标量位；利用有限差分法，根据标量位计算标量位 水平方向的二阶导数；利用拉普拉斯方程，根据标量位水平方向的二阶导数得到标量位的 垂直方向的二阶导数；重复上述计算过程，得到重磁数据的各阶垂向导数。 在一些实施方式中，利用波数域的重磁数据换算方法计算重磁数据的标量位，包 括：根据如下公式计算重磁数据的标量位： 其中，F表示傅里叶变换，F-1表示傅里叶逆变换，kx,ky表示与空间域坐标x,y对应 的波数域坐标，z0表示重磁数据在垂向坐标z的高度位置，  u(x,y,z0)是观测高度为z0的重 5 CN 111580174 A 说　明　书 3/11 页 磁数据， 表示波数域垂向积分算子，v(x,y,z0)表示换算得到的重磁数据的标量 位。 在一些实施方式中，利用有限差分法，根据标量位计算标量位水平方向的二阶导 数，包括：根据如下公式计算标量位水平方向的二阶导数： 其中，Δx与Δy均表示水平方向的采样间距，vxx表示x轴方向的二阶导数，vyy表示 y轴方向的二阶导数。 在一些实施方式中，利用拉普拉斯方程，根据标量位水平方向的二阶导数得到标 量位的垂直方向的二阶导数，包括：根据如下公式计算标量位的垂直方向的二阶导数： uz(x,y,z0)＝vzz(x,y,z0)＝-[vxx(x,y,z0) vyy(x,y,z0)] 其中，uz表示重磁数据垂直方向的一阶导数，vzz表示标量位垂直方向的二阶导数， vxx及vyy表示标量位的水平方向的二阶导数。 在一些实施方式中，利用各阶垂向导数计算帕德近似的系数方程，并求解系数方 程的系数，包括：利用二阶垂向导数计算帕德近似的系数方程，并求解系数方程的系数。 在一些实施方式中，利用二阶垂向导数计算帕德近似的系数方程，并求解系数方 程的系数，包括：根据如下公式计算系数方程的系数： 其中，p0、q1、q2为帕德近似的系数方程中的系数，c0、c1、c2为各阶垂向导数。 在一些实施方式中，利用求得的系数代入帕德近似，计算重磁数据的向下延拓结 果，包括：根据如下公式计算重磁数据的向下延拓结果： 其中，h表示向下延拓的高度，u(x,y,z0 h)表示重磁数据的向下延拓结果，u(x,y, z0)表示重磁数据。 采用这样的设计后，本发明至少具有以下优点： 本发明提供的一种基于积分垂向导数的帕德近似重磁数据向下延拓方法，与传统 方法相比，本发明利用帕德近似直接对重磁数据进行函数逼近，而不是间接逼近，计算简 单、直观。本发明的帕德近似是2阶的有理逼近，在逼近理论上其精度比泰勒级数展开高，而 且在泰勒级数展开不收敛的情况也可以保证收敛，提高了向下延拓结果的准确性。采用的 积分二次垂向导数方法计算导数，有效增强了换算的稳定性和准确性。本发明中的帕德近 似具有不同阶次的表达公式，本发明为了实现直观，选择计算误差更小、更稳定的二阶帕德 6 CN 111580174 A 说　明　书 4/11 页 近似，实现重磁数据的稳定且准确的向下延拓。 附图说明 上述仅是本发明技术方案的概述，为了能够更清楚了解本发明的技术手段，以下 结合附图与