技术摘要：
本发明提供肌肉协同的提取方法及基于肌肉协同的运动功能分析评估方法。人体运动过程中采集多块肌肉的表面肌电信号，预处理后得到多通道肌电数据矩阵D，利用多元曲线分辨‑交替最小二乘对不同协同数下的方差占比进行分析，方差占比大于等于80％的最小协同数k为最终协同  全部
背景技术：
中枢神经系统如何控制身体的肌肉骨骼系统完成日常各种复杂的肢体动作一直 是众多学者研究的焦点和热点。而肌肉协同理论能够较好地解释中枢神经系统对于肌肉骨 骼系统的控制机制。 一个肌肉协同是由多块不同激活强度的肌肉组成，而一块肌肉可在多个肌肉协同 中被激活。人体的各种复杂肢体动作能够通过少数几个肌肉协同在时域上的叠加控制完 成。因此，肌肉协同可用于分析、评估人体的运动功能。 目前，肌肉协同主要通过矩阵分解算法分析多通道肌电数据计算得到。非负矩阵 分解是应用最为广泛的肌肉协同提取方法，该方法首先随机产生初始协同和激活矩阵，并 由重构矩阵与原始数据矩阵的残差构建目标函数，最后通过迭代优化的方式不断缩小重构 矩阵与原始数据矩阵之间的残差，直到达到收敛条件停止迭代，实现肌肉协同的提取。非负 矩阵分解具有原理简单、容易实现、分解结果非负性的优点。该方法的计算过程存在稀疏性 约束，因此对于稀疏协同具有较好的分析效果。但是对于肌肉群普遍肌张力保持较高水平 的个体而言，例如脑卒中、脊髓损伤等患者，其肌肉协同难以保证稀疏性。此外，人体很多多 自由度运动的肌肉协同也是非稀疏的。在这些情况下非负矩阵分解法容易陷入局部最优， 重复性较差，难以获得准确的肌肉协同。因此，稳定、可靠的肌肉协同提取方法具有重要的 意义。
技术实现要素：
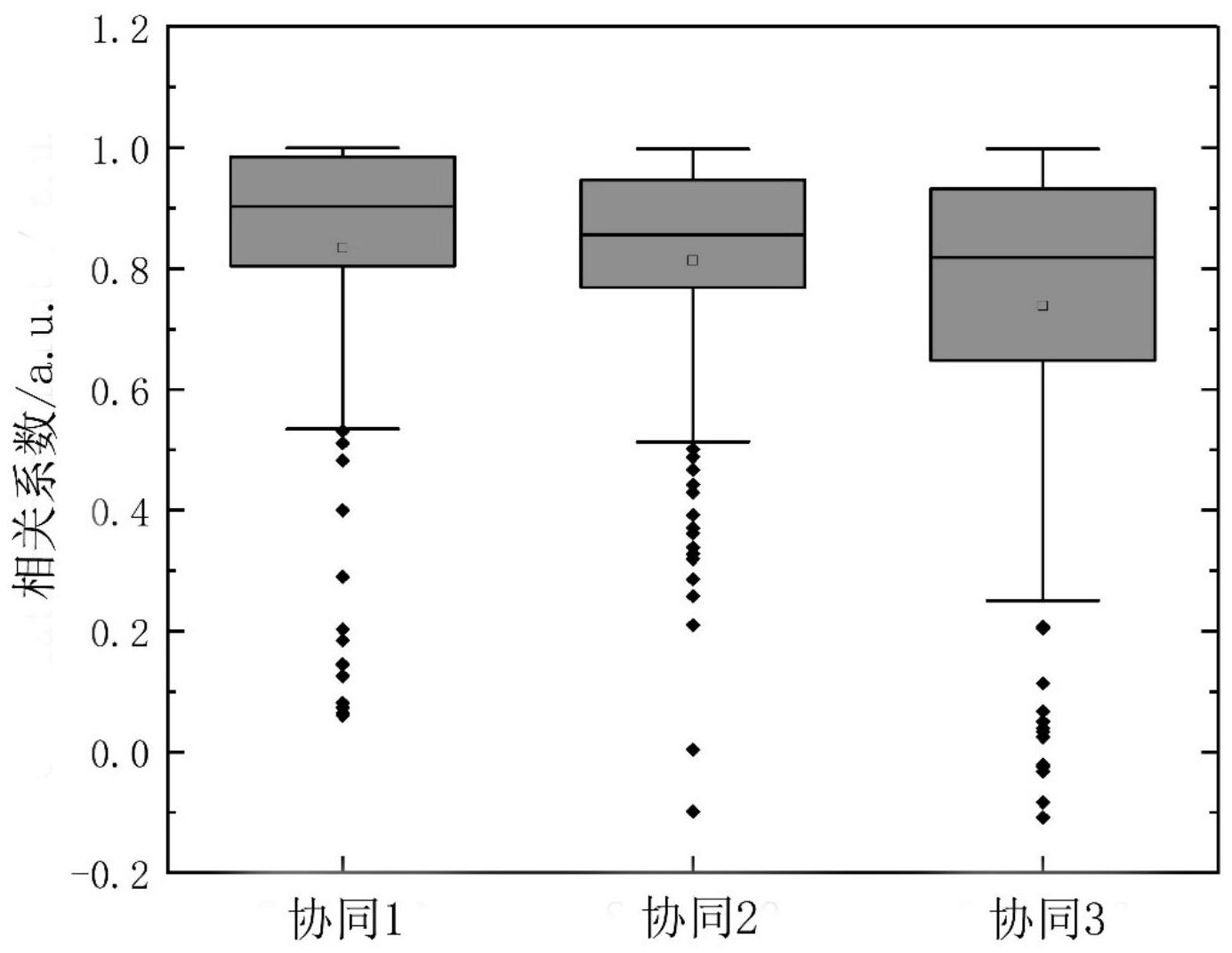
针对上述技术现状，本发明人经过大量的试验探索后发现，采用多元曲线分辨-交 替最小二乘法提取的肌肉协同具有唯一性，大大提高了肌肉协同提取的稳定性和准确性， 对运动功能的分析评估具有重要意义。 即，本发明的技术方案为： 一种肌肉协同提取方法，包括如下步骤： (1)人体运动过程中采集多块肌肉的表面肌电信号，预处理后得到多通道肌电数 据矩阵D(m×n)，m为肌电数据的通道数，n为肌电数据的变量数； (2)通过分析多通道肌电数据矩阵D(m×n)，提取肌肉协同； 其特征是：所述的步骤(2)中，采用多元曲线分辨-交替最小二乘法提取肌肉协同， 即，针对肌电数据矩阵D(m×n)，利用多元曲线分辨-交替最小二乘法在不同协同数下的方 差占比进行分析，方差占比大于80％的最小协同数k为最终协同数，2≤k≤m，再利用多元曲 线分辨-最小二乘法从肌电数据矩阵D中提取k个肌肉协同。 4 CN 111543990 A 说　明　书 2/6 页 2、如权利要求1所述的基于肌肉协同的运动功能分析评估方法，其特征是：所述步 骤(2)包括如下： (2-1)确定第1个纯变量 对于变量j，1≤j≤n，其平均值μj和均方差σj分别为： 其中，dij是肌电数据矩阵D中第i行、第j列的元素； 根据(式1)(式2)计算第1个纯度谱，第1个纯度谱中的第j(1≤j≤n)个元素为p1,j： 其中，α是矫正参数，对信号噪声有一定的抑制作用，其值为1到5的常数； 在第1个纯度谱中，假设第t1个元素纯度最大，则变量t1(1≤t1≤n)为第1个纯变 量； (2-2)确定第i个纯变量，2≤i≤k 首先利用变量长度λ对肌电数据矩阵D进行归一化，肌电变量j的长度λj为： 归一化后的肌电数据矩阵D(λ)中第i行、第j列元素为： d(λ)i,j＝di,j/λj    (式5) 计算COO(Correlation  around  the  origin)矩阵E： E＝(1/m)D(λ)TD(λ)    (式6) 根据COO矩阵E，纯变量j的相关行列式为： 其中，t1为第一个纯变量，ω2 ,j作为权重系数用于计算第2个纯度谱，根据(式1) (式2)(式7)计算第2个纯度谱，第2个纯度谱中的第j个元素为p2,j，1≤j≤n： 在第2个纯度谱中，假设第t2个元素值最大，则变量t2为第2个纯变量，1≤t2≤n； 以此类推，对于i≥2时，相关行列式表示为： 对于i≥2时，第i个纯度谱中的第j个元素为pi,j，2≤i≤k，1≤j≤n： 5 CN 111543990 A 说　明　书 3/6 页 在第i个纯度谱中，假设第ti个元素值最大，则变量ti为第i个纯变量，1≤ti≤n； (2-3)假设协同数k＝2； (2-4)从肌电数据矩阵D中提取出所有纯变量(t1,t2,…,tk)对应位置的元素，组成 初始协同矩阵S(m×k)，然后利用交替最小二乘(式11和式12)迭代优化，使目标函数(式13) 值最小， C＝(STS)-1(STD)    (式11) S＝(DCT)(CCT)-1    (式12) 再利用式14计算方差占比VAF(Variance  account  for)： VAF＝1-(||D-SC||2/||D-mean(D)||2)    (式14) (2-5)当步骤(2-4)计算得到的方差占比小于80％时，协同数k增加1，重复步骤(2- 1)、(2-2)、(2-4)，直到计算得到的方差占比大于或等于80％，对应的协同数k即为最终协同 数，在该协同数下计算得到的矩阵S为最终的肌肉协同。 所述肌肉不限，包括上肢肌肉、下肢肌肉等。 本发明中的肌肉协同计算方法基于多元曲线分辨-交替最小二乘，包括纯变量计 算、协同初始化矩阵、迭代优化等，首先计算各肌电信号变量的纯度谱，将成分贡献率较高 的变量提取出来构建初始化协同矩阵，避免了传统非负矩阵分解法的随机初始化，然后基 于初始化协同矩阵，利用交替最小二乘法优化分析结果，使多元曲线分辨的重构数据与原 始数据更接近。与现有的非负矩阵分解法提取的肌肉协同相比，具有如下有益效果： (1)对于非稀疏肌肉协同的提取具有更好的准确性和稳定性； (2)无需重复运行程序寻找最小残差的分解结果，因此运行速度快于非负矩阵分 解法； (3)利用本发明提取得到的肌肉协同进行人体运动功能分析、评估、预测、控制时 可提高相应的准确性与稳定性。 附图说明 图1是本发明实施例1中受试者A的数据矩阵D1经非负矩阵分解法重复计算20多次 得到的肌肉协同统计盒须图。 图2是本发明实施例1中受试者A的数据矩阵D1经非负矩阵分解法以及多元曲线分 辨-交替最小二乘法重复提取的肌肉协同统计图。