技术摘要：
本发明旨在提供基于空间归化的最短路径求解方法，包括以下步骤：将路网归化到矢量地理空间，获得起始地与目的地；以起始地与目的地连线中心为圆点，以起始地与目的地连线的长度为直径，构建包含起始地和目的地的第一圆；找出第一圆内所有的路径，并将这些路径进行拓扑  全部
背景技术：
最短路径问题一直是计算机科学和地理信息科学中的经典问题，传统的类似问题 解决多采用经典计算机算法如蚁群算法、A*算法、Dijkstra算法等，Dijkstra算法可以求解 出数学最优解，但效率低；其他算法效率高，但却解算不出数学最优解，各种算法的解决思 维不尽相同，因此很难兼顾优和准的问题，研究的方向也分为两个主流方向：Dijkstra算法 的搜索效率优化和其他算法的精准度提升--至今没有学者能够统一两者，将其他算法的高 效率与Dijkstra算法的数学严谨求解和二为一。 最短路径问题的解困扰计算机图形学、数学、逻辑学、地理信息科学等多个学科领 域数十年，其研究解决的方向出现异化，需要效率难于顾及精准度，需要精准度难于顾及效 率，因此该领域的研究走入死胡同至今无法解决这一矛盾。由简单数学分析可知，最短路径 必然存在，其特点是路径上任意两点间的距离也是最短，是局部解和整体解得有机统一，因 此研究自然分化为确保局部和确保整体两个方向。 由最短路劲的存在性和几何特点可知，问题最终就是长度比较，长度比较实质是 线问题求解，而线是面的边界，因此可以通过将其他算法求解的问题归化到几何空间，通过 几何手段完成样本空间的减缩优化，之后再利用Dijkstra算法求解最优解，最终实现所有 最短路径算法在空间领域的统一，达到最短路径搜索“快”与“准”的统一。
技术实现要素：
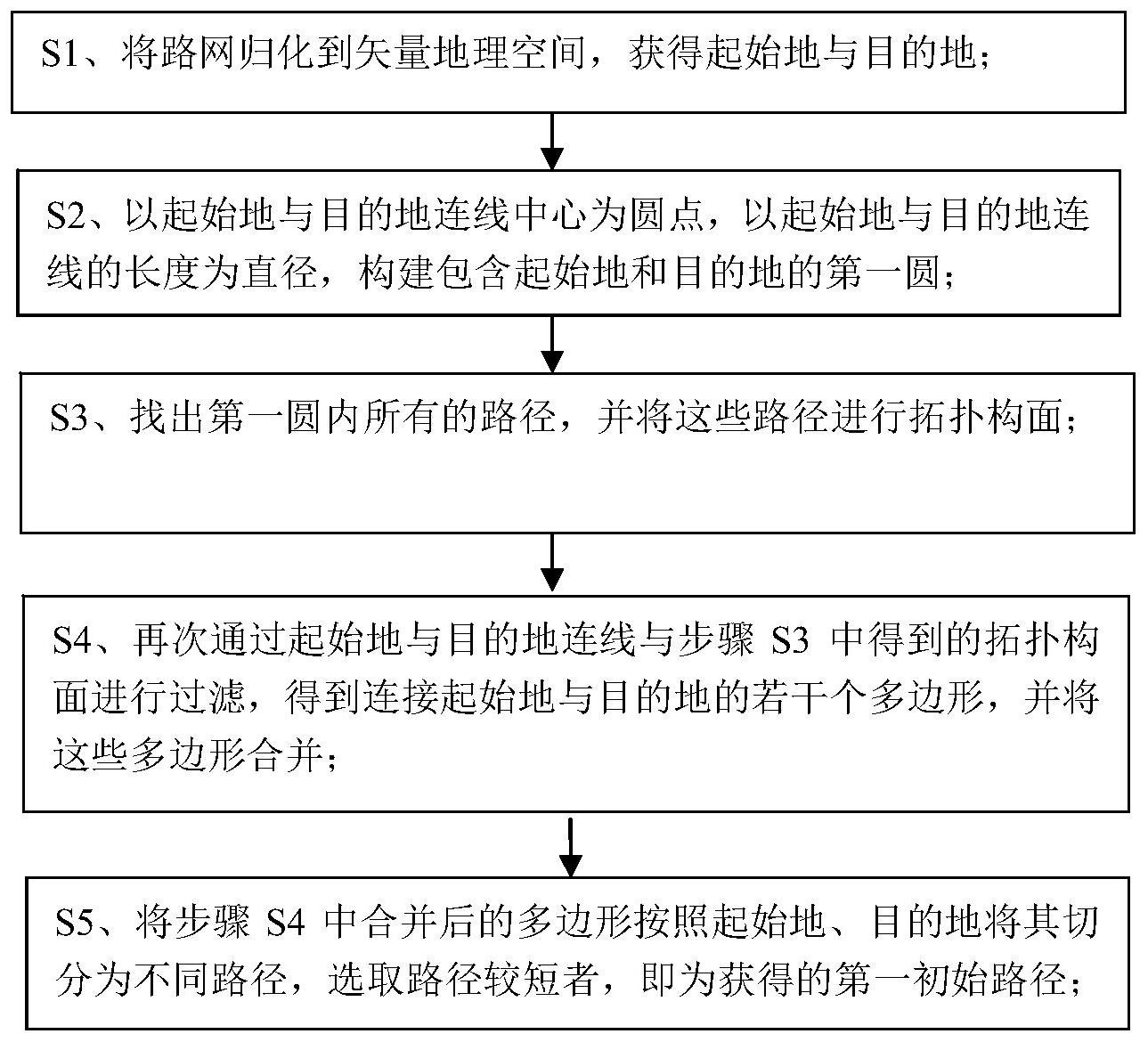
有鉴于现有技术的上述缺陷，为实现上述目的，本发明提供了一种基于空间归化 的最短路径求解方法，以约束最短路径求解时解空间的发散问题，包括如下步骤： S1、将路网归化到矢量地理空间，获得起始地与目的地； S2、以起始地与目的地连线中心为圆点，以起始地与目的地连线的长度为直径，构建包 含起始地和目的地的第一圆； S3、找出第一圆内所有的路径，并将这些路径进行拓扑构面； S4、再次通过起始地与目的地连线与步骤S3中得到的拓扑构面进行过滤，得到连接起 始地与目的地的若干个多边形，并将这些多边形合并； S5、将步骤S4中合并后的多边形按照起始地、目的地将其切分为不同路径，选取路径较 短者，即为获得的第一初始路径。 作为可选的改进技术方案：步骤S3中还包括：只要路径在圆内或与圆有交叉，均筛 选出来进行拓扑构面。 作为可选的改进技术方案：还包括步骤S6、以第一初始路径长度为基准，将起始地 与目的地的连线中心为圆心构建第二圆，将第二圆范围内过滤出来的路径进行拓扑构面， 3 CN 111612257 A 说　明　书 2/5 页 获取第二初始路径，将第二初始路径与第一初始路径进行比对，验算第一初始路径的准确 性。 作为可选的改进技术方案：步骤S6还包括如下步骤： S61、以此起点和终点连线即第一初始路径长度为直径，以起点和终点连线的中心为圆 点，构建第二圆； S62、找出第二圆圆内所有的路径，并将这些路径进行拓扑构面； S63、再次通过起点与终点连线与步骤S62中得到的拓扑构面进行过滤，得到连接起点 与终点的若干多边形，并将这些多边形合并； S64、将步骤S63中合并后的多边形按照起点、终点将其切分为不同路径，选取路径较短 者，即为获得的第二初始路径； S65、将第二初始路径与第一初始路径进行比对，以验算第一初始路径的准确性。 作为可选的改进技术方案：步骤E2中还包括：只要路径在圆内或与第二圆有交叉， 均筛选出来进行拓扑构面。 特别地，所述的步骤B中圆的构建过程原因分析如下： 在步骤S2中通过构建以起始地与目的地连线长度为直径的第一圆，将问题从距离长度 的一维空间拓展到二维空间，通过二维空间的范围概念约束可能解的空间，进而求出初始 解，即第一初始路径。 步骤S3实现功能在于： 通过构面将问题的解空间拓展到二维面领域，合并多边形的目的为迅速找出可以包含 起始地与目的地的面，进而找出可能的问题解，同时也为后续计算机的循环优化提供理论 说明及初始值。 步骤S4与S5实现功能在于： 利用二维面是闭合线的概念，通过合并多边形将起始地、目的地、面、线结合在一起，通 过闭合线找到初始解，进而为后期继续压缩解空间进而求解真值提供便利。 步骤S6实现功能在于： 通过步骤S5求的初始解是近似解，真值长度必然在两点连线和此近似解范围内。通过 该近似解再次构建范围圆，由几何分析可知该范围圆内必然包含真值，进而再次约束和确 保接真解求解的有效、快速、准确。 本发明将传统计算机图形学、逻辑学中对于最短路径求解统一归化到地理空间范 畴，通过几何学、空间科学等相关技术，将参与解算的路径局限在小范围内。该范围与目标 点连线线性相关，与全局样本数无关，因此也就解决了Dijkstra算法样本空间优化问题。借 助升维降维思维，长度问题就是一维逻辑问题，而空间分析技术就是二维空间对象的逻辑 判定技术，因此利用空间分析技术，将整体问题求解转化为局部问题求解进而求得最终解， 也解决了其他算法如生物算法、智能算法只能求得局部最优解难于求解整体最优解的难 题，是近年来将空间科学思维用于统一最短路径求解的新尝试。 最短路径是二维环境下的一维问题，因此其求解复杂度不低于样本数的二次方。 对于二维环境下的一维问题，必然存在一维和二维的关联，这种关联就是隐含的二维环境 下的对象拓扑关系。本发明构建范围圆，其实质就是将距离的解空间从一维拓展到约束的 二维的过程，因此以升维降维思维为引导，借助拓扑关系这一维度之间的关联，有可能将二 4 CN 111612257 A 说　明　书 3/5 页 维问题一维化，进而快速求解出一维问题解。 本发明将弥补传统的A*算法估价函数选取困难问题，解决蚁群算法、遗传算法、神 经网络算法等只能求解近似解无法完成数学最优解的难题。与专利ZL201510790636.5相 比，本发明是该专利的前置，是将一维问题二维化过程中的全局二维化变革为局部二维化 过程，优势在于不需要将全局样本进行二维拓扑构面，节约了大量的存储空间和计算资源， 为实时最短路径分析的实现提供技术支持。 附图说明 图1为本发明的流程图。 图2为实施例中原始路线示意。 图3为实施例中以直接连线构建过滤范围圆的示意图。 图4为实施例中过滤得到的所有路径构面的示意图。 图5为实施例中通过连线过滤连接起始点多边形的示意图。 图6为实施例中找出构面后的多边形合并后导入空间坐标系后的矢量化图。 图7为实施例中以起终点为圆焦点，初始解长度为基准构建的圆示意图。 图8为实施例中图5的圆范围压盖的道路区域示意图。 图9为实施例中的最优解示意图。 图10至图12为通过椭圆来约束搜索范围的示意图。 图13为通过圆来约束搜索范围的示意图。