技术摘要：
本发明公开了一种铝合金薄壁构件耦合加工稳定性控制方法，将铝合金粉末铺于工作台，用激光器对选区进行激光烧结；按“铺粉—烧结”环节，循环十次；使用有限元方法获取烧结后金属片以及机床系统的动力学参数；建立考虑再生效应的状态空间形式的铣削动力学微分方程，将  全部
背景技术：
铝合金由于其良好的材料力学性能被广泛应用于航空航天制造业，而具有复杂形 状的铝合金薄壁构件制备是先进制造技术领域的一个热点和难点。切削加工是从毛坯上切 除多余的材料而形成最终零件的方法，包括车、铣、钻、刨、磨等。传统的以铣削为代表的减 材制造其材料利用率低，加工效率低；增材制造的原理是通过材料的不断叠加而形成零件， 而单纯的增材制造难以保证增材制造过程的表面质量。因此，在铝合金薄壁构件制造过程 中采用“激光增材制造-精密铣削加工”耦合成型来获得高质量、高精度的零件的方法受到 广泛关注。而在对激光烧结后的材料表面进行铣削时，由于激光烧结后形成的金属薄片具 有壁薄，刚性差等特点，在铣削时极易发生切削颤振，严重影响金属薄片表面加工质量，极 易造成报废。对于传统的机床颤振问题，国内外众多学者对其产生机理与预测方案进行了 较为深入的研究，但对于激光烧结后形成的金属薄片的精密铣削振动问题尚未见系统研 究。 传统的解决方案是以经验法和试错法为主的降低切削用量法，主要是降低轴向切 削深度，调整主轴转速。但此类做法是以牺牲加工效率来获得加工质量的方法，限制了生产 效率。
技术实现要素：
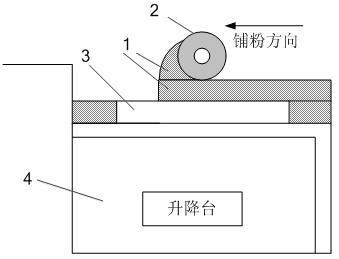
为了解决铝合金薄壁构件激光增材制造与高速铣削耦合加工过程中表面加工振 动问题，本发明提供一种铝合金薄壁构件耦合加工稳定性控制方法，将Cotes数值积分计算 铣削稳定性的方法应用于解决铝合金薄壁构件激光增材制造与高速铣削耦合加工过程中， 获得无颤振条件下的最佳切削用量组合来确保金属薄片表面铣削过程的稳定性，解决表面 加工振动问题，最终实现复杂铝合金薄壁构件的精确快速成型。 本发明采用以下技术方案实现上述目的。一种铝合金薄壁构件耦合加工稳定性控 制方法，其步骤如下： 步骤一：首先使用铺粉装置通过滚轮将铝合金粉末均匀地铺撒在工作台上，工作 台与升降台联动可以上下移动，并控制铺粉厚度等于工艺设计层厚； 步骤二：升降台带动工作台下降，滚轮退回，工作台上升至铺粉高度，由激光器发 生激光束对金属粉末选区进行激光烧结得到金属薄片； 步骤三：按“铺粉—烧结”环节，循环十次； 步骤四：使用有限元方法获取烧结后金属片以及机床系统的动力学参数； 步骤五：建立考虑再生效应的状态空间形式的铣削动力学微分方程： 7 CN 111597661 A 说　明　书 2/10 页 具体步骤如下： S01:首先考虑再生效应的n个自由度的铣削动力学微分方程可以表述为： 其中，M、C和K为刀具系统的n个自由度的模态质量矩阵、模态阻尼矩阵和模态刚度 矩阵，q(t)是刀具n个自由度的振动位移矢量，Kc(t)为系统所受动态铣削力矩阵，t为连续 时间，T为单个刀齿切削周期，ap是轴向切削深度； S02:令 方程(1)转换为状态空间形式： 其中： 步骤六：将一个周期内的连续时间t表示为离散的时间节点： ti＝t0 tf (i-1)τ；    (3) 式(3)中，i＝1,2,...,m,m 1.t0为开始切削时刻，tf自由振动时间段，τ为离散间隔 长度,m为单个周期离散数； 步骤七：计算在区间[ti,ti 1]内的方程(2)表达式： 其具体步骤如下： S03:将状态方程的apB(t)[x(t)-x(t-T)]看作齐次方程 的非齐次项， s为计算过程中的积分因子，则可以将方程(2)表示为如下形式： S04:根据式(4)可知，当ti≤t≤ti 1时，可以得到在区间[ti,ti 1]内的表达式如下： 步骤八：计算关于状态项x1，x2和x3的等式： 8 CN 111597661 A 说　明　书 3/10 页 具体步骤如下： S05:当刀具不切削的时刻，即在时间段tf内，此时B(s)为0，方程(5)退化为 S06:为了公式表示的简洁性，下文统一使用xi代替x(ti)，xi-T代替x(ti-T)，Bi代替 B(ti)，Bi-T代替B(ti-T)； S07:在t1＝t0 tf时刻，由式(3)和(5)可以很容易得到以下关于状态项x1的等式： S08:在离散点t2处，状态项x2可以表示为： S09:由梯形求积公式，可以得到状态项x2的近似表达公式： S10:移项整理后，分离出状态项和时滞项如下式： S11:类似地，在离散点t3处，状态项x3可以得到： S12:由Simpson求积公式，可以得到x3的近似表达式为： S13:同样，分离状态项和时滞项可得到： 步骤九：计算关于状态项x4的等式 9 CN 111597661 A 说　明　书 4/10 页 S14:与S11步骤类似，在离散点t4处，状态项x4可以得到： S15:由Newton求积公式，分离状态项和时滞项可以得到： 步骤十：计算第t5到tm 1点的求积公式： 其中： 具体步骤如下： S16:第t5到tm 1点的求积公式可表示为： 其中，i＝1,2,…,m-3； S17:由Cotes求积公式，分离状态项和时滞项可以得到： 步骤十一：得到系统在一个周期内的状态转移矩阵，表示为F -1IM＝G H， 10 CN 111597661 A 说　明　书 5/10 页 其中， 具体步骤如下： S18:联立式(6)、(9)、(12)、(14)和(16)得到如下离散映射： Gym 1＝Hym 1-T；    (17) S19:系统在一个周期内的状态转移矩阵表示为： F ＝G-1IM H；    (18) 步骤十二：计算状态转移矩阵FIM的特征值，通过判断特征值的模的大小来判断稳 定性，具体公式为： 最终以主轴转速为横坐标，轴向切深为纵坐标进行绘图； 步骤十三：依据步骤十二计算结果结合机床实际情况得到最合适的铣削参数组合 对烧结后的表面进行高速铣削；选择铣削加工参数时在曲线下方稳定区域选择对应的主轴 转速和轴向切深进行铣削加工，即可获得无颤振切削情况；在曲线上方不稳定区域选择主 轴转速和轴向切深进行铣削加工，则会发生切削颤振； 11 CN 111597661 A 说　明　书 6/10 页 步骤十四：重复步骤一到步骤十三直至零件加工制造完毕。 本发明通过理论计算获得其在铣削加工时加工失稳的临界轴向切削深度，计算得 到关于主轴转速和轴向切深的二维稳定性极限图，在铣削烧结后的金属薄片时，按照Cotes 数值积分方法计算得到的最优无颤振切削参数来设置切削用量以实现稳定切削，并且实现 最大材料去除效率。 附图说明 图1是本发明中实施例步骤一铺粉流程的示意图； 图2是本发明中实施例步骤二激光烧结增材制造示意图； 图3是本发明中实施例步骤十四计算得到的烧结后薄壁构件铣削稳定性图； 图4是本发明中实施例步骤十五高速铣削烧结后的金属薄片示意图； 图5是本发明的控制流程图。