技术摘要：
本发明提供一种基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪方法，包括：构建雷达状态方程和雷达量测方程、雷达状态先验更新方程和雷达量测先验更新方程；根据雷达状态方程、雷达状态先验更新方程和雷达量测方程构建雷达系统非线性模型；根据k 1时刻雷达目标点迹的量测  全部
背景技术：
在雷达跟踪系统中，由于目标位置的量测通常是距离、方位角、俯仰角等信息，而 这些信息一般是在极坐标系得到的，这就使得雷达跟踪系统必然是非线性的。对于非线性 滤波问题，目前最常用的滤波算法有扩展卡尔曼滤波(EKF)、不敏卡尔曼滤波(UKF)以及粒 子滤波(PF)等。而在雷达量测系统中，往往又存在重尾非高斯噪声，而目前处理非高斯噪声 的滤波算法则有学生t滤波、Huber’s  M估计滤波等方法。然而，常用的非线性滤波方法在高 斯假设下可以取得很好的滤波效果，但在非高斯情况下则出现滤波恶化等问题。而处理非 高斯噪声的滤波方法则又会出现参数选择困难、计算复杂等问题。 对于非线性、非高斯滤波问题，本发明将最大相关熵扩展卡尔曼滤波(MCEKF)应用 到雷达跟踪系统中，该滤波方法采用最大相关熵准则(MCC)而非传统的最小均方误差准则 (MMSE)作为优化准则，相比于传统准则只能得到误差二阶项信息，该准则不仅可以获得误 差二阶项信息，还可以捕捉滤波误差的高阶统计量，从而使得系统跟踪性能得到极大改善， 降低了系统跟踪性能在重尾非高斯噪声下严重恶化的影响。 为了方便描述，下面首先介绍雷达跟踪系统中的滤波系统模型。 雷达跟踪系统中的滤波模型包括离散状态方程和离散量测方程。对于雷达来说， 目标的状态信息通常是在直角坐标系下获得的，而量测信息则是在空间极坐标系下获得 的，所以将雷达系统中的直角坐标系记为雷达直角坐标系OXYZ，极坐标系记为雷达极坐标 系，其对应关系图1中所示。 雷达直角坐标系下离散时间系统的状态方程为， X(k 1)＝f(X(k)) V(k)    (1) 其中，X(k 1)为k 1时刻目标运动的状态向量，f(·)为目标运动的状态转移函数， V(k)为k时刻目标运动的过程噪声，且假定过程噪声服从零均值的高斯分布，其方差为， E[V(k)VT(j)]＝Q(k)δkj    (2) 其中， Q(k)为k时刻的过程噪声的协方差矩阵。 雷达极坐标系下离散时间系统的量测方程为， 5 CN 111596290 A 说　明　书 2/14 页 其中，Z(k 1)＝[r(k 1) θ(k 1)  φ(k 1)]T，x(k 1)、y(k 1)和z(k 1)分别为k 1 时刻目标在直角坐标系中x轴、y轴以及z轴的位置，r(k 1)、θ(k 1)和φ(k 1)分别为目标在 k 1时刻的径向距离、方位角以及俯仰角的雷达量测信息，W(k 1)为量测噪声，其方差为， E(W(k 1)WT(j 1))＝R(k 1)δkj    (5) 其中，R(k 1)为时刻k 1的量测噪声协方差矩阵，δkj的定义同式(3)。 其次介绍最大相关熵准则(MCC)。 最大相关熵是度量两个随机变量 之间相似性的一个重要的信息论量。假 设它们的联合分布函数为FXY(x,y)，它们之间的相关熵定义为， V(X,Y)＝E[κ(X,Y)]＝∫κ(x,y)dFXY(x,y)    (6) 其中，E代表期望算子，κ(·，·)代表平移不变的Mercer核。在本发明中，所有的核 函数是均是由高斯核函数给出的。其表达式为， 其中e＝x-y，σ＞0代表核带宽。 然而，在大多数雷达跟踪系统中，只有有限个数据可用，所以变量之间的联合概率 密度FXY通常情况下是未知的。在这种情况下，可以使用样本均值对相关熵进行估计。具体形 式是， 这里e(i)＝x(i)-y(i)， 是从联合概率密度函数FXY中抽取的N个样本。 对高斯核进行泰勒级数展开，可以得到， 可以看出，相关熵是X-Y所有偶阶矩的加权和，从中能够提取数据的高阶统计量。 需要注意，当核带宽很大时，二阶矩将对相关熵起主要作用。 给定误差数据序列,基于MCC准则下的代价函数为：
技术实现要素：
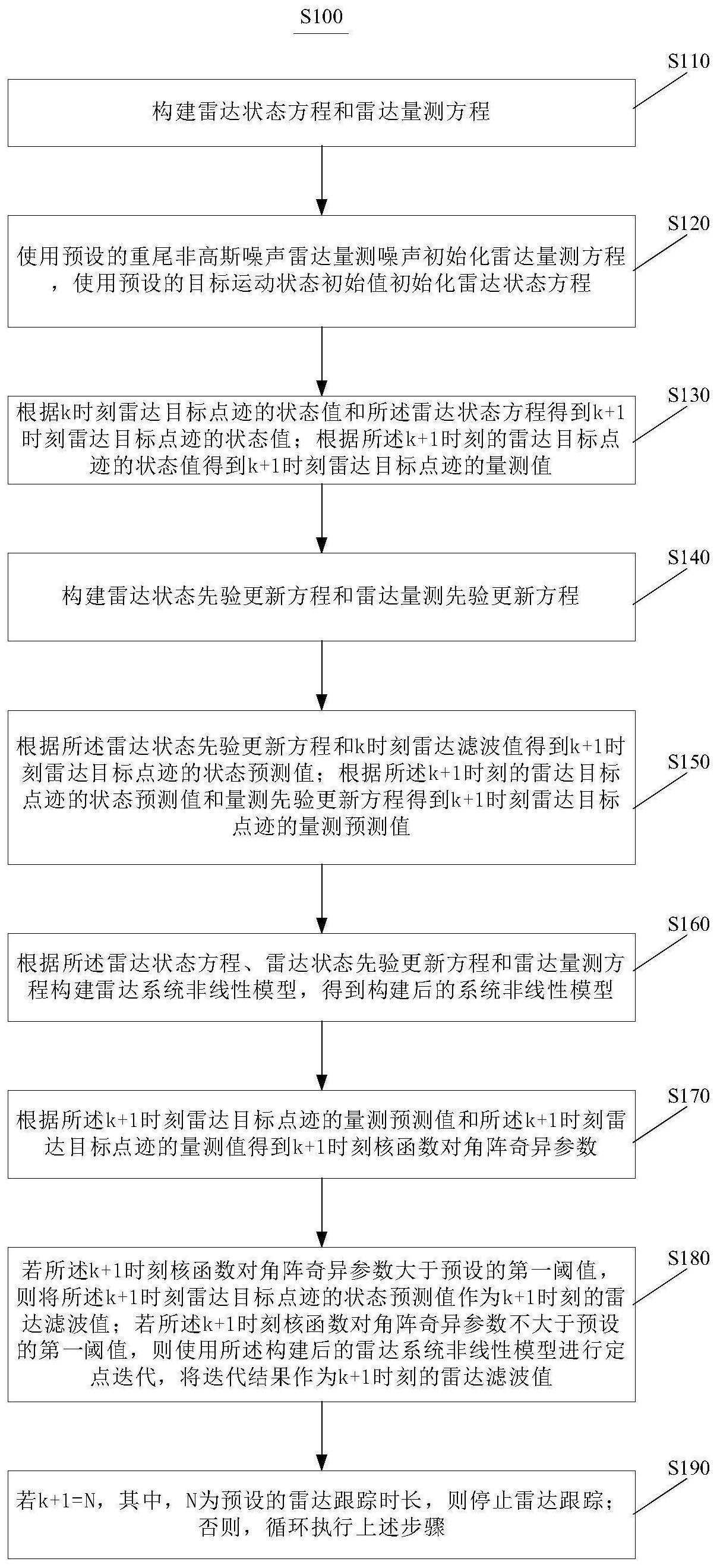
本发明旨在至少解决现有技术中存在的技术问题之一，提供一种基于最大相关熵 扩展卡尔曼滤波的雷达目标跟踪方法。 6 CN 111596290 A 说　明　书 3/14 页 本发明的一个方面提供一种基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪方 法，包括： 构建雷达状态方程和雷达量测方程； 使用预设的重尾非高斯噪声雷达量测噪声初始化雷达量测方程，使用预设的目标 运动状态初始值初始化雷达状态方程； 根据k时刻雷达目标点迹的状态值和所述雷达状态方程得到k 1时刻雷达目标点 迹的状态值； 根据所述k 1时刻的雷达目标点迹的状态值得到k 1时刻雷达目标点迹的量测值； 构建雷达状态先验更新方程和雷达量测先验更新方程； 根据所述雷达状态先验更新方程和k时刻雷达滤波值得到k 1时刻雷达目标点迹 的状态预测值； 根据所述k 1时刻的雷达目标点迹的状态预测值和量测先验更新方程得到k 1时 刻雷达目标点迹的量测预测值； 根据所述雷达状态方程、雷达状态先验更新方程和雷达量测方程构建雷达系统非 线性模型，得到构建后的系统非线性模型； 根据所述k 1时刻雷达目标点迹的量测预测值和所述k 1时刻雷达目标点迹的量 测值得到k 1时刻核函数对角阵奇异参数； 若所述k 1时刻核函数对角阵奇异参数大于预设的第一阈值，则将所述k 1时刻雷 达目标点迹的状态预测值作为k 1时刻的雷达滤波值；若所述k 1时刻核函数对角阵奇异参 数不大于预设的第一阈值，则使用所述构建后的雷达系统非线性模型进行定点迭代，将迭 代结果作为k 1时刻的雷达滤波值； 若k 1＝N，其中，N为预设的雷达跟踪时长，则停止雷达跟踪；否则，循环执行上述 步骤。 可选的，所述构建雷达状态方程、雷达状态先验更新方程、雷达量测方程，包括： 雷达状态方程：X(k 1)＝f(X(k)) V(k) 雷达量测方程： Z(k 1)＝h(X(k 1)) W(k 1) 其中， X(k 1)为k 1时刻雷达目标点迹的状态值； X(k)为k时刻雷达目标点迹的状态值； V(k)为k时刻雷达目标运动的过程噪声； f(·)为雷达目标点迹的状态转移函数； Z(k 1)为在k 1时刻雷达目标点迹的量测值； x(k 1)、y(k 1)和z(k 1)分别为k 1时刻雷达目标在直角坐标系中x轴、y轴以及z 轴的位置； 7 CN 111596290 A 说　明　书 4/14 页 W(k 1)为k 1时刻雷达目标点迹的量测噪声； h(·)为雷达目标量测的非线性函数。 可选的，根据所述雷达状态方程、雷达状态先验更新方程和雷达量测方程构建雷 达系统非线性模型，得到构建后的雷达系统非线性模型，包括： 重组所述雷达状态方程、雷达状态先验更新方程和雷达量测方程，得到非线性模 型组成参量； 根据所述非线性模型组成参量的协方差矩阵得到Cholesky分解参量； 根据所述Cholesky分解参量得到构建后的雷达系统非线性模型。 可选的，所述重组所述雷达状态方程、雷达状态先验更新方程和雷达量测方程，得 到非线性模型组成参量，包括； 所述非线性模型组成参量为： 可选的，所述根据所述非线性模型组成参量的协方差矩阵得到Cholesky分解参 量，包括： 其中，M(k 1)为Cholesky分解参量，R(k 1)为k时刻雷达目标点迹的量测噪声协方 差矩阵 可选的，所述根据所述Cholesky分解参量得到构建后的雷达系统非线性模型： D(k 1)＝B(X(k 1)) e(k 1) 其中，非线性模型的第一参量为： 非线性模型的第二参量为： 非线性模型的第三参量为：e(k 1)＝M-1(k 1)α(k 1) 可选的，根据所述k 1时刻雷达目标点迹的状态预测值和所述k 1时刻雷达目标点 迹的量测值得到k 1时刻核函数对角阵奇异参数，包括： β(k 1)＝ψT(k 1)η-1(k 1)ψ(k 1) 8 CN 111596290 A 说　明　书 5/14 页 其中， 为k时刻雷达目标点迹的量测预测值； Z(k 1)为k时刻雷达目标点迹的量测值； 为 的协方差； hX(k)为k时刻雷达目标量测的非线性函数h(·)的雅可比矩阵； β(k 1)为k 1时刻核函数对角阵奇异参数。 可选的，所述使用所述构建后的雷达系统非线性模型进行定点迭代，包括： 根据k 1时刻雷达目标点迹的状态预测值得到k 1时刻迭代初始值； 根据k 1时刻雷达目标量测的非线性函数的雅可比矩阵得到k 1时刻迭代量测矩 阵； 使用所述构建后的雷达系统非线性模型和预设的高斯核带宽，构建k 1时刻高斯 核函数，根据所述k 1时刻高斯核函数得到对应的k 1时刻高斯核函数对角阵； 根据所述迭代初始值和迭代量测矩阵对所述k 1时刻高斯核函数对角阵进行至少 一次迭代，得到每次迭代的结果； 判断所述每次迭代的结果是否符合预设的第二阈值，若是，则停止迭代，得到对应 的迭代结果。 可选的，使用所述构建后的雷达系统非线性模型和预设的高斯核带宽，构建k 1时 刻高斯核函数，包括： 其中，σ为高斯核带宽， 为k 1时刻t-1次迭代的迭代参数。 可选的，所述根据所述k 1时刻高斯核函数得到对应的k 1时刻高斯核函数对角 阵，包括： 其中，x代表前n个高斯核函数，y代表后m个高斯核函数。 本发明实施例的一种基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪方法中，对 于非线性、非高斯滤波问题，本发明将最大相关熵扩展卡尔曼滤波(MCEKF)应用到雷达跟踪 系统中，该滤波方法采用最大相关熵准则(MCC)而非传统的最小均方误差准则(MMSE)作为 优化准则，相比于传统准则只能得到误差二阶项信息，该准则不仅可以获得误差二阶项信 息，还可以捕捉滤波误差的高阶统计量，从而使得系统跟踪性能得到极大改善，降低了系统 跟踪性能在重尾非高斯噪声下严重恶化的影响。在雷达跟踪中，使用最大相关熵扩展卡尔 曼滤波的雷达目标跟踪方法既可以实现非线性跟踪系统的滤波，又可以有效降低非高斯重 尾噪声使雷达跟踪性能严重恶化的影响，相比于传统的非线性滤波方法，其跟踪性能及其 鲁棒性得到极大改善。 9 CN 111596290 A 说　明　书 6/14 页 附图说明 图1为本发明一实施例的基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪方法的 流程图； 图2为本发明一实施例的雷达极坐标与雷达直角坐标对应关系示意图； 图3为本发明一实施例的基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪滤波位 置均方根误差仿真结果图； 图4为本发明一实施例的基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪滤波速 度均方根误差仿真结果图； 图5为本发明一实施例的基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪滤波位 置均方根误差仿真结果图； 图6为本发明一实施例的基于最大相关熵扩展卡尔曼滤波的雷达目标跟踪滤波速 度均方根误差仿真结果图。