技术摘要：
本发明公开了一种基于几何重建模型的等几何分析方法，包括步骤：将CAD模型的边界划分为三角形面片或直接根据点云数据，生成一个封闭的规则嵌入域，并将嵌入域划分为规则的子域；根据三角形面片边界/点与单元的位置关系，将单元分为裁剪单元和非裁剪单元；计算裁剪单元  全部
背景技术：
等几何分析方法由Hughes提出，采用一种用于几何模型和计算机模型相同的基函 数完成计算机辅助设计和工程分析，成为了一种高效的数字化分析方法。因为采用与CAD相 同的基函数，等几何分析是构建CAD模型和工程分析的高效方法。并且等几何分析方法具有 低计算机性能耗用和高精度的优越性，因此等几何分析被广泛运用于各种模型和工程分 析。然而，CAD的边界表示形式和张量积曲线曲面结构使得等几何分析三维复杂几何模型具 有很大难度。等几何分析最重要的部分是获取模型的样条模型参数化模型。在实际应用中， 一个复杂的分析模型是不可能用一个完整张量积形式的样条模型来表示的，这使得等几何 分析不能直接应用于具有复杂拓扑结构的工程模型。此外，CAD系统通常使用边界表示方法 来表示几何对象，在CAD系统中不存在用于三维问题的三维样条。为了解决上述难题以及工 程分析中存在的问题，需要一种可基于边界多边形或点云来表示复杂几何模型的方法，以 及基于该模型表示实现等几何分析的方法。
技术实现要素：
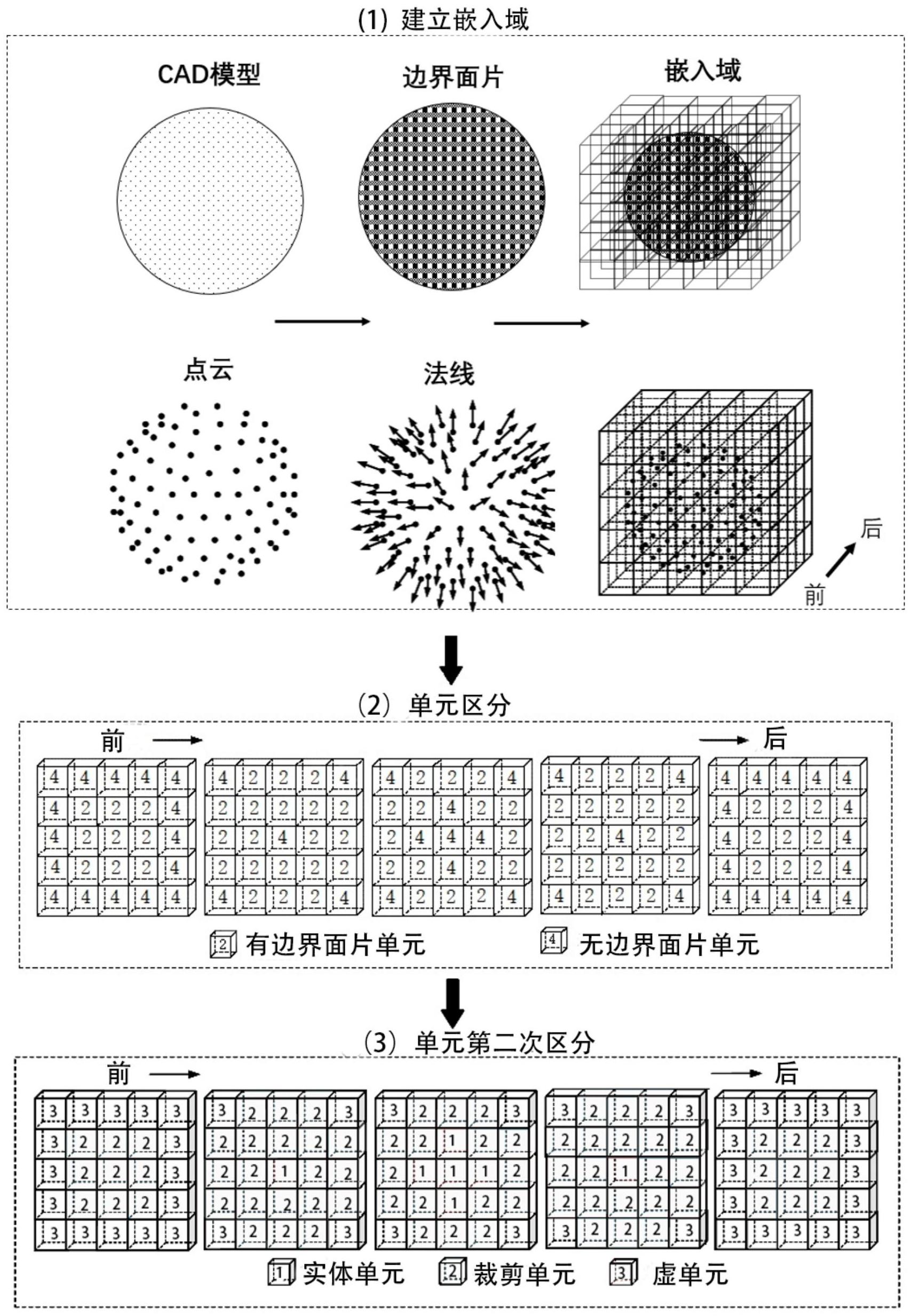
本发明的目的在于克服现有技术的不足，提供一种基于几何重建模型的等几何分 析方法。 本发明的目的能够通过以下技术方案实现： 一种基于几何重建模型的等几何分析方法，包括步骤： 将CAD模型的边界划分为三角形面片，基于三角形面片边界生成一个封闭的规则 嵌入域，并将嵌入域划分为规则的子域，即单元；对于点云可基于点建立嵌入域； 根据三角形面片边界/点与单元的位置关系，将单元分为两类：内部有面片边界/ 点的单元(裁剪单元)和内部没有面片边界/点的单元(非裁剪单元)； 计算裁剪单元各顶点到该裁剪单元附近三角形面片的最小有向距离； 获得最小有向距离后，利用有向距离把非裁剪单元划分为实单元和虚单元； 将最小有向距离作为水平集函数值，运用移动四面体算法基于规则嵌入域重建一 个显示的几何模型； 获得水平集函数值后，计算出单元内高斯点的水平集函数值，若此值大于等于零， 则该高斯点在实域内；若此值小于零，则该高斯点在实域外。计算单元刚度矩阵只需要实域 内的高斯点。 进一步地，所述将CAD模型的边界划分为三角形面片，基于三角形面片边界生成一 个封闭的嵌入域，并将嵌入域划分为规则的子域的步骤中，所述单元尺寸应大于三角形面 片尺寸。 4 CN 111581776 A 说　明　书 2/5 页 进一步地，所述基于三角形面片边界生成一个封闭的规则嵌入域，生成方法为：通 过所有三角形面片顶点在坐标轴的最大最小值，即Xmax、Xmin、Ymax、Ymin、Zmax、Zmin，构建一个尺 寸为(Xmax-Xmin)×(Ymax-Ymin)×(Zmax-Zmin)的规则长方体包围盒将所有三角形面片包含其 中，该包围盒占据的空间就是嵌入域。 对于点云模型，直接获取点云中各点在坐标轴的最大最小值后采用相同方法构建 嵌入域。 进一步地，所述根据面片边界与单元的位置关系，将单元分为两类的步骤中，单元 划分依据为：若单元内包含任意三角形面片的顶点或中心，则该单元为内部有边界面片的 单元(裁剪单元)；反之，则为没有边界面片的单元(非裁剪单元)。对于点云构建的嵌入域划 分的单元，若单元内包含任意点，则该单元为内部有点的单元(裁剪单元)；反之，则为没有 点的单元(非裁剪单元)。 进一步地，所述计算裁剪单元各顶点到该裁剪单元附近三角形面片的最小有向距 离的步骤中，依次在各三角形面片上找到一点到单元顶点P距离最近，计算该点到P点的距 离，选出其中的最小值得到最小距离，最小距离的正方向确定为顶点到三角形面片的方向， 根据最小距离方向与面片外向量方向之间的关系将最小距离转化为有向距离。 对于点云，计算裁剪单元顶点到点的距离并选出最小距离。点云的外法线可由3D 扫描仪获得。根据顶点到最近点的方向与该点外向量，可将最小距离转化为有向距离。 进一步地，所述获得裁剪单元顶点最小有向距离后，利用该有向距离把非裁剪单 元划分实单元和虚单元，划分方法为：由裁剪单元的邻接非裁剪单元开始，若该非裁剪单元 含有最小有向距离为正值的顶点，则该非裁剪单元为实单元；若该非裁剪单元含有最小有 向距离为负值的顶点，该非裁剪单元为虚单元；依此方式，再用已分类的非裁剪单元逐层扩 展到其他未分类的非裁剪单元，直到所有非裁剪单元分类完成。 更进一步地，对未分类的非裁剪单元逐层扩展的方法为：对裁剪单元顶点所共享 的非裁剪单元进行扩展，然后再依次对其他非裁剪单元进行扩展，扩展原则是：若该非裁剪 单元任意一个顶点的最小有向距离为负值，则该非裁剪单元的所有顶点的最小有向距离均 设为该负值，该非裁剪单元则为虚单元(即该单元位于嵌入模型边界外部)；若该非裁剪单 元任意一个顶点的最小有向距离为正值，则该非裁剪单元的所有顶点的最小有向距离均设 为该正值，该非裁剪单元则为实单元(即该单元位于嵌入模型边界内部)。 进一步地，所述重建几何模型的步骤中，将裁剪单元细分为六个四面体，此时四面 体各个顶点的有向距离已知，对于顶点最小有向距离既有正值又有负值的四面体，运用线 性插值法计算出四面体各边上的最小有向距离为零的交点，连接各交点，形成一个有向距 离为零的平面。将所有单元依据上述方法构造零平面，组合后即得到重建的几何模型。这个 重建模型可用于模型加工制造。 进一步地，所述获得水平集函数值后，计算出单元高斯点的水平集函数值的步骤 中，水平集值大于零的高斯点需要保留用于计算单元刚度矩阵，水平集值小于零的高斯点 去掉不参与刚度矩阵计算。 本发明相较于现有技术，具有以下的有益效果： 1 .本发明基于水平集函数隐式近似重构模型，可快速识别嵌入域中的单元类型， 无需繁琐的CAD求交技术。 5 CN 111581776 A 说　明　书 3/5 页 2.本发明通过将几何模型嵌入能被CAD样条函数直接表达的规整嵌入域，通过重 构模型可直接实现等几何分析，解决了现有等几何分析难以直接分析复杂几何模型的技术 瓶颈。 3 .本发明可直接对点云模型进行等几何分析，而无需根据点云显示重建几何模 型。 附图说明 图1为本发明中获取设计模型的离散边界表示方法的示意图。 图2为本发明中将单元划分为有边界面片单元和无边界面片单元方法的示意图。 图3为本发明中实虚单元扩展的示意图。 图4为本发明中求取有向距离方法的示意图。 图5为本发明中移动四面体算法的示意图。 图6为本发明中判断高斯点是否在实域内方法的示意图。