技术摘要：
本发明实施例公开了一种丝锥螺纹加工的磨削轨迹优化方法及系统，其特征在于，包括：S1、创建磨削轨迹坐标系并获取相邻两段螺纹的二维曲线方程；S2、创建相邻两段螺纹对应的过渡曲线二维计算模型以获取二维螺纹加工轨迹；S3、获取二维螺纹加工轨迹上每一点在刀具轴方向  全部
背景技术：
丝锥是加工圆柱形和圆锥形内螺纹的标准刀具，其应用范围广泛，种类多种多样。 由于丝锥的磨削损耗较大，一般都是大批量的生产和出售，但它对加工精度的要求很高。对 丝锥的加工一般都是通过丝锥磨床实现的，目前国外的丝锥磨床发展迅速，诸如多线丝锥 磨床、整体磨制工艺的使用等都在一定程度上提高了丝锥的生产效率，使得加工精度和性 能得到了保证。同时随着数控技术的发展，数控丝锥磨床也已问世，通过数字控制多轴联动 使得丝锥的加工更加简单，进一步提升生产效率，是丝锥目前的生产趋势。 但是需要说明的是：为了提高市场竞争力，就需要大幅提高丝锥的生成效率、产品 精度及性能，汇总一个最有效的方法就是提高丝锥磨床的切削速度和磨削精度等，但如果 其速度过大，可能造成丝锥表面的灼伤。
技术实现要素：
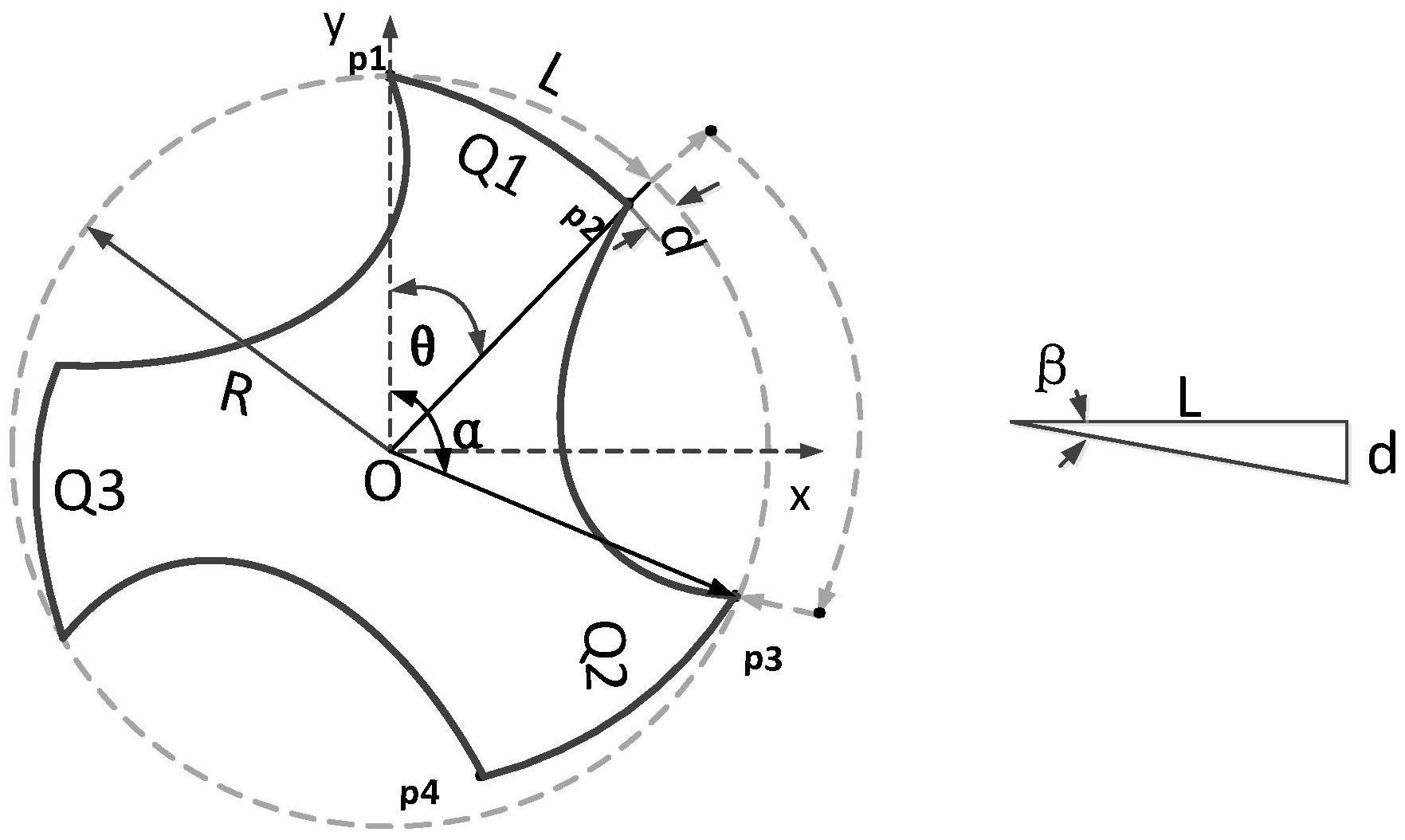
基于此，为解决现有技术存在的不足，特提出了一种丝锥螺纹加工的磨削轨迹优 化方法。 一种丝锥螺纹加工的磨削轨迹优化方法，其特征在于，包括： S1、创建磨削轨迹坐标系并获取相邻两段螺纹的二维曲线方程，其中，所述磨削轨 迹坐标系是以刀具中心O为原点所建立的坐标系{O；x,y}，该坐标系下任意曲线对应的参数 方程的表达式为： f(r,t)＝{r*sint,r*cost} 上式中，半径r为曲线上的任意点到坐标原点的距离，夹角t为该点所对应的曲线 的径向方向与坐标轴y所构成的夹角，所述径向方向是指从坐标原点指向该点的方向向量； 所述相邻两段螺纹中的第一段螺纹Q1的二维曲线方程为： f1(t)＝f(r(t) ,t)＝{(R-R*tanβ*t)*sint,(R-R*tanβ*t)*cost} r(t)＝R-R*tanβ*t； 上式中，第一段螺纹曲线Q1的半径r和夹角t的关系式：r1(t)＝R-R*tanβ*t，R为刀 具半径，该段螺纹的降角β对应的表达式为β＝arctan(d/L)，d为螺纹的降量，磨削角度θ对 应的弧长L＝R*θ*π/180； 所述相邻两段螺纹中的第二段螺纹Q2的二维曲线方程为： f2(t)＝f(r(t) ,t)＝{(R-R*tanβ*(t-α))*sint,(R-R*tanβ*(t-α))*cost} 上式中，第二段螺纹曲线Q2的半径r和夹角t的关系式：r2(t)＝R-R*tanβ*t(t-α)， 相邻两螺纹间的分度角为α＝2*π/n，n为切削刃个数； S2、确定相邻两段螺纹过渡部分半径r与夹角t的关系方程以创建相邻两段螺纹对 4 CN 111571316 A 说　明　书 2/8 页 应的过渡曲线二维计算模型，其中，所述关系方程对应的方程表达式为： 上式中，上一段螺纹Q1终点处的夹角t1对应的表达式为t1＝θ，半径r1对应的表达 式为r1＝R-R*tanβ*θ，半径r1对应的导数r1′对应的表达式为r1′＝-R*tanβ；下一段螺纹Q2 终点处的夹角t2对应的表达式为t2＝α，半径r2对应的表达式为r2＝R，半径r2对应的导数 r2′对应的表达式为r2′＝-R*tanβ；将所述关系方程代入上述参数方程即获得过渡曲线二 维计算模型以获取二维螺纹加工轨迹； S3、获取二维螺纹加工轨迹上每一点在刀具轴方向上的坐标分量与该点夹角的关 系方程以获得三维空间下对应的螺纹磨削加工轨迹，所述坐标分量z与夹角t对应表达式 为； 上式中，P为螺距。 此外，为解决现有技术存在的不足，还提出了一种丝锥螺纹加工的磨削轨迹优化 系统，其特征在于，包括： 第一轨迹计算单元，该单元能够创建磨削轨迹坐标系并获取相邻两段螺纹的二维 曲线方程，其中，所述磨削轨迹坐标系是以刀具中心O为原点所建立的坐标系{O；x,y}，该坐 标系下任意曲线对应的参数方程的表达式为： f(r,t)＝{r*sint,r*cost} 上式中，半径r为曲线上的任意点到坐标原点的距离，夹角t为该点所对应的曲线 的径向方向与坐标轴y所构成的夹角，所述径向方向是指从坐标原点指向该点的方向向量； 所述相邻两段螺纹中的第一段螺纹Q1的二维曲线方程为： f1(t)＝f(r(t) ,t)＝{(R-R*tanβ*t)*sint,(R-R*tanβ*t)*cost} r(t)＝R-R*tanβ*t； 上式中，第一段螺纹曲线Q1的半径r和夹角t的关系式：r1(t)＝R-R*tanβ*t，R为刀 具半径，该段螺纹的降角β对应的表达式为β＝arctan(d/L)，d为螺纹的降量，磨削角度θ对 应的弧长L＝R*θ*π/180； 所述相邻两段螺纹中的第二段螺纹Q2的二维曲线方程为： f2(t)＝f(r(t) ,t)＝{(R-R*tanβ*(t-α))*sint,(R-R*tanβ*(t-α))*cost} 上式中，第二段螺纹曲线Q2的半径r和夹角t的关系式：r2(t)＝R-R*tanβ*(t-α)， 相邻两螺纹间的分度角为α＝2*π/n，n为切削刃个数； 第二轨迹计算单元，该单元能够确定出相邻两段螺纹过渡部分半径r与夹角t的关 系方程以创建相邻两段螺纹对应的过渡曲线二维计算模型，其中，所述关系方程对应的方 程表达式为： 5 CN 111571316 A 说　明　书 3/8 页 上式中，上一段螺纹Q1终点处的夹角t1对应的表达式为t1＝θ，半径r1对应的表达 式为r1＝R-R*tanβ*θ，半径r1对应的导数r1′对应的表达式为r1′＝-R*tanβ；下一段螺纹Q2 终点处的夹角t2对应的表达式为t2＝α，半径r2对应的表达式为r2＝R，半径r2对应的导数 r2′对应的表达式为r2′＝-R*tanβ；将所述关系方程代入上述参数方程即获得过渡曲线二 维计算模型以获取二维螺纹加工轨迹； 螺纹磨削加工轨迹获取单元，该单元能够获取二维螺纹加工轨迹上每一点在刀具 轴方向上的坐标分量与该点夹角的关系方程以获得三维空间下对应的螺纹磨削加工轨迹， 所述坐标分量z与夹角t对应表达式为； 上式中，P为螺距。 实施本发明实施例，将具有如下有益效果： 本发明提出了一种丝锥的螺纹工序加工过程中，从一段螺纹结束点和下一段螺纹 开始点之间砂轮的磨削轨迹优化方案，其通过创建磨削轨迹坐标系并获取相邻两段螺纹的 二维曲线方程，创建相邻两段螺纹对应的过渡曲线二维计算模型等步骤保证了两段螺纹间 的轨迹过渡是光滑的，从而在不影响加工质量的前提下，优化了丝锥的辅助加工路径，减少 辅助加工的时间，大幅度地提高了加工效率。 附图说明 为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现 有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本 发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以 根据这些附图获得其他的附图。 其中： 图1(a)为一个实施例中丝锥结构的侧视图； 图1(b)为一个实施例中丝锥结构的正视图； 图2为一个实施例中丝锥螺纹的二维轨迹示意图； 图3为一个实施例中螺纹曲线和过渡曲线的r与t的关系图； 图4为一个实施例中二维螺纹曲线和过渡曲线图； 图5(a)和(b)分别为直槽丝锥和螺旋丝锥的螺纹磨削轨迹图； 图6为一个实施例中丝锥螺纹工序的基本参数； 图7为一个实施例中丝锥螺纹工序的过渡参数； 图8为一个实施例中采用直线过渡的加工时间； 图9为一个实施例中采用圆弧过渡的加工时间； 图10(a)和(b)为一个实施例中所示方法获得丝锥成品效果图。 6 CN 111571316 A 说　明　书 4/8 页