技术摘要：
一种电力系统即插即用的稳定性分析与控制方法，利用仿真估计方法离线估计子系统的LIOS属性，其中，LIOS属性包括局部稳定域以及渐近增益；通过基于邻接矩阵法的分布式信息采集算法，获取全部子系统的LIOS属性信息，利用稳定性准则判断含可再生能源的电力系统的稳定性，  全部
背景技术：
随着经济社会的发展，我国能源需求持续增长，能源资源和环境问题日益突出，加 快开发利用可再生能源已成为我国应对日益严峻的能源环境问题的必由之路。然而，含可 再生能源的电力系统运行工况复杂多变，电力系统中的潮流分布具有强随机性和不确定 性，容易引发节点电压越限与线路过载等多种问题。可再生能源发电设备大多采用电力电 子接口并网，其固有的弱惯性特点可能恶化电力系统的阻尼特性，引发系统动态响应恶化 等问题，甚至引发暂态失稳与电压崩溃。这些问题严重制约了可再生能源在我国电力系统 中的大规模应用。 为了最大限度的接纳与利用可再生能源，电力系统应该具有“即插即用”的特点。 因此，有必要提出一种适应含可再生能源的电力系统“即插即用”的稳定性分析与控制方 法，为含可再生能源的电力系统的运行提供指导。 稳定性分析是含可再生能源的电力系统“即插即用”功能的核心，其为新能源发电 设备及其他动态设备的接入与退出提供接口条件。目前，时域仿真法广泛用于电力系统的 稳定性分析，虽然时域仿真可以对系统进行精确的稳定性评估，但是其计算量较大，并且无 法获得系统稳定裕度等量化分析结果。Lyapunov理论为电力系统的稳定性分析提供另一种 途径，通过计算初始状态到给定稳定区域边界的距离可以得到量化的稳定性分析结果。然 而，由于缺乏用于构造Lyapunov函数的一般性算法使得该理论难以应用于一般非线性系 统，同时，Lyapunov理论研究对象自治系统，无法量化分析外部扰动对系统的影响。 研究非线性系统稳定性的另一种途径是输入-状态稳定性(ISS)理论，ISS理论将 Lyapunov方法和输入-输出稳定理论相结合，将互联系统分解为若干子系统，然后利用子系 统的ISS特性及其连接关系研究互联系统的稳定性。“分解”的思想赋予ISS理论灵活性和快 速性，适用于含可再生能源的电力系统“即插即用”场景。
技术实现要素：
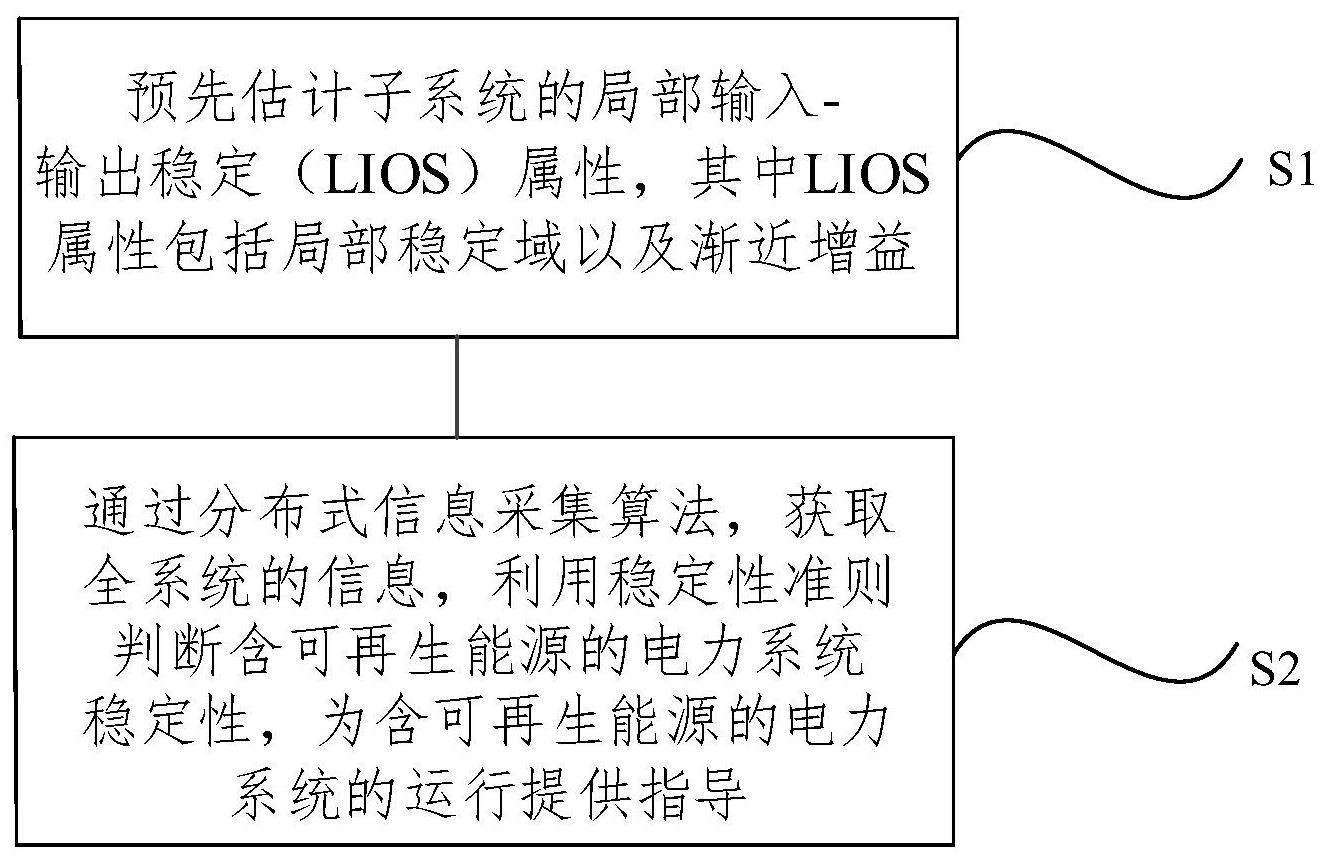
本发明的目的是提供一种电力系统即插即用的稳定性分析与控制方法。 为实现上述目的，本发明采用如下的技术方案： 一种电力系统即插即用的稳定性分析与控制方法，包括如下步骤： S1，利用仿真估计方法离线估计子系统的LIOS属性，其中，LIOS属性包括局部稳定 域以及渐近增益； S2，通过基于邻接矩阵法的分布式信息采集算法，获取步骤S1估计的全部子系统 的LIOS属性信息，利用稳定性准则判断含可再生能源的电力系统的稳定性，为可再生能源 的接入与退出提供接口条件。 6 CN 111555311 A 说　明　书 2/13 页 本发明进一步的改进在于，步骤S1中，利用仿真估计方法离线估计子系统的LIOS 属性的具体过程为： 第1步，选择子系统的状态变量x以及输出y； 第2步，参考子系统的保护配置，给定子系统的安全运行约束； 第3步，给定输入信号u，固定子系统的初始状态x0，得到输出y； 取t→∞时刻输出信号的稳态值，此时β＝0，输入-输出增益近似估计为： 其中，ye为输出平衡点，ue为输入平衡点，t为时间； 第4步，改变输入信号u的幅值，计算输入-输出增益，得到一系列的γ，从一系列的 γ中取最大的γ近似作为子系统的输入-输出增益； 第5步，在第4步估计的子系统输入信号的范围内，改变子系统的初值以及输入；计 算β≈|y-ye|-γmax||u-ue||∞，利用指数函数β，取最大值以及末端的稳定点进行拟合，时刻 分别为tmax，tend，幅值分别为ymax，yend，其中，tmax，tend分别指最大时间和最终时间，ymax，yend 分别指最大输出和最终输出，则有 从而计算得出最大输出ymax的待定系数和最终输出yend的待定系数λ和K； 从而得到子系统的LIOS属性。 本发明进一步的改进在于，第4步中，如果状态变量、输出的值超过给定的安全运 行约束，认为此时子系统失稳；逐步减小输入直至子系统稳定，估计子系统输入信号的范 围。 本发明进一步的改进在于，步骤S2中，通过基于邻接矩阵法的分布式信息采集算 法，获取步骤S1估计的全部子系统的LIOS属性信息的具体过程如下： 第一步，每个子系统以标准格式存储全系统中所有发电机、负载、线路的数据信 息；对第i个子系统，初始状态向量为y 0i ，元素个数等于全系统中所有发电设备、负载设备与 线路设备数量之和，除去第i个元素，其它位置以0代替；各子系统形成各自的信息状态向 量： 7 CN 111555311 A 说　明　书 3/13 页 该信息状态向量包括各子系统的ISS属性和初始状态； 第二步，每个子系统利用以下定理1和相邻的子系统交换彼此信息，直到每个子系 统前后两次信息通讯的系统的系统状态向量完全一致，此时各子系统获得全系统的状态信 息； 定理1对任意一个n节点系统，设每个节点i的状态向量为yi的阶数由n决定，对yi进 行迭代运算，即 其中，y ki 表示yi经过k次迭代后的结果，式中所有加法和乘法均为布尔加和布尔 乘，布尔加和布尔乘定义为： b b＝b；b 0＝b；0 0＝0 其中，b为任意的实数。 本发明进一步的改进在于，含有外部输入的非线性系统： 其中，状态变量x∈Rn，Rn为n维实数域，输入变量y∈Rp，u∈Rm，f：Rn×m→Rn，h：Rn×m→ Rp，Rp为p维实数域，Rm为m维实数域，Rn×m为n×m维实数域，f和h在x和u中是连续的局部 Lipschitz，f(0，0)＝0，h(0，0)＝0； 对含有外部输入的非线性系统，若存在β∈KL、 对于任何初始状态和外 部输入，满足以下不等式 则该系统是ISS的；其中，|·|表示Euclidean范数，||·||表示矩阵的范数，||u| |∞是使得|u(t)|≤a对于所有的时间t均成立的最小的a； 为比较函数。 本发明进一步的改进在于，一个函数γ：R≥0→R≥0，若满足连续、严格单增以及γ (0)＝0，则称之为 函数；若γ函数满足当s→∞时，γ(s)→∞，则称之为 函数；一个 函数β：R≥0×R≥0→R≥0，若满足连续条件，且对于任一固定的t≥0，函数β(·，t)是 函数，β (s，t)关于t是递减的，并且当t→∞时，β(s，t)→0，则称β(s，t)为 函数。 本发明进一步的改进在于，步骤S2中，利用稳定性准则判断含可再生能源的电力 系统的稳定性，为可再生能源发电设备及动态负荷的接入与退出提供接口条件的具体过程 如下： 由n个子系统组成的动态系统，第i个子系统的数学模型如下所示 yi＝hi(xi，ui，ωi) 其中， 是第i个子系统的状态变量， 和 分别是子系统 的输入与输出， 为mi阶实数， 为Pi阶实数，ωi是子系统受到的外部扰动输入； 假设第i个子系统满足LISS和LIOS，即存在函数 8 CN 111555311 A 说　明　书 4/13 页 以及实数vi，τi＞0，使得对于任意时间t≥0，|xoi|≤vi和||ui||∞≤τi，如下条件满足 |xoi|≤νi和||ui||∞≤τi同时使得上述条件成立，因此并不需要输出变量yi对状态 量xi可观，yj，j＝1，…，n作用于子系统i时，形成的输入ui满足||ui||∞≤τi； 由n个子系统互联而成的全系统数学模型如下 0＝g(y，u) 其中，x＝[x  …  x ]T1 n ∈RN，N＝n1 … nn，u＝[u1  …  u ]Tn ∈Rm，m＝m1 … mn，y＝ [y1…yn]T∈Rp，p＝l1 … ln； 如果满足以下四个条件，则全系统是LIOS和LISS的； (1)当|xoi|≤νi，||ui||∞≤τi，||ωi||∞≤εi时，每个子系统是LISS和LIOS的，并且 具有线性的渐近增益； (2)函数g(y，u)满足隐函数定理： ui＝si(yi，…，yn) 其中，ui为系统i的输入，si为网络方程，yi系统i的输出； 存在zii≥0，di≥0，使得下式满足 |ui(t)|≤∑zij(|yj(t)|) di 其中，zij为电力系统网络方程，di为与拓扑有关的系数； (3)满足如下小增益条件 ρ(GIOS)＜1 其中，GIOS＝ΓIOSZ，ΓIOS是形如 的输入/输出增益矩阵；ρ表示 矩阵GIOS的谱半径； (4)下述条件成立 |xoi|≤vi，||ωi||∞≤εi且|ui[t＝0]|＜τi； 其中，τ＝[τ  … τ]T，d＝[d  …  d ]T，βIOS1 n 1 n ((|xo|)c，0)＝(βi(|xoi|，0)，i＝1，…， n)T， Z为电力系统网络方程矩阵，d为与拓扑有关的系数矩 阵， 为小增益矩阵，βIOS((|xo|)c，0)为βIOS的初始状态矩阵。 9 CN 111555311 A 说　明　书 5/13 页 本发明进一步的改进在于，对于任意x ∈ΩIOS∈Rn0 ，u∈UIOS∈Rm，ΩIOS为状态域， UIOS为扰动域，如果存在比较函数 对于任何初始状态和外部输 入，满足以下不等式： 则含有外部输入的非线性系统是LIOS的，其中βIOS和γIOS分别为比较函数。 本发明进一步的改进在于，对于任意x0∈ΩISS∈Rn，u∈UISS∈Rm，ΩISS为状态域， UISS为扰动域，如果存在比较函数 对于任何初始状态和外部输 入，满足以下不等式： 则含有外部输入的非线性系统是LISS的；其中，βISS和γISS分别为比较函数。 与现有技术相比，本发明具有的有益效果：本发明通过分布式信息采集，每个子系 统都可以获得全系统的信息，并利用稳定性分析方法判断系统稳定性，为动态设备的接入 与退出提供接口条件。利用解耦的思想分析含可再生能源的电力系统的稳定性，具有灵活 性和快速性，为含可再生能源的电力系统“即插即用”提供指导，保障系统的安全稳定运行。 并且仿真结果与计算结果相吻合。 附图说明 图1为含可再生能源的电力系统示意图。 图2为计算光伏LIOS属性流程图。 图3为分布式信息采集过程中的系统信息矩阵。 图4为箅例一仿真结果。 图5为箅例二仿真结果。 图6为本发明的总体流程图。