技术摘要：
本发明公开了一种考虑空间大变形的介入手术导丝建模方法及其应用，步骤如下：将导丝离散成有限个梁单元；单个梁单元以节点位移矢量与位移场的斜率矢量作为广义坐标，通过节点位移矢量、节点斜率矢量描述导丝变形和导丝截面转动，推导得到单个梁单元的总动能和总势能的  全部
背景技术：
微创心血管介入手术，以其减少术后疼痛、缩短恢复时间、创伤小等优点广泛使 用，其中导丝作为关键介入器械要深入到心脏冠状动脉腔壁变狭窄或阻塞处。虚拟现实技 术作为提升临场感的关键技术被应用到介入手术中，通过虚拟现实技术，重构一个与现实 手术系统环境完全一致的虚拟现实环境，操作者直接通过人机交互设备与虚拟现实环境交 互，即时产生视觉、听觉、触觉、力觉等感官感受。 柔性线缆模型表达是进行虚拟环境下介入手术仿真的基础，该模型不仅要支撑导 丝的几何特性，还要支持物理特性表达，并满足虚拟现实系统特有的实时性要求。导丝的特 点是长度远大于其直径。由于导丝的形状不像刚体那样固定不变，而是随着外界条件的不 同发生改变，因此建模难度很大。 介入手术操作过程中，导丝和血管壁移动接触存在大范围的摩擦受力，主端使用 虚拟现实技术进行其物理形变特征的实时仿真是一个有挑战的工作。而手术器械与血管壁 碰撞的检测检测是非常耗时的，碰撞检测算法的好坏很大程度上决定了系统的整体性能。 介入手术中导丝在工作时进行大范围运动，必须使用动力学方法对其进行描述和 计算。将必须考虑弹性变形影响的部件作为柔性体处理，进行有限元离散，保留有限自由 度。对于导丝等细长物体的物理形变实时仿真，一般将导丝沿长度方向进行离散化，分析各 微元的形变及受力。 现有的介入导丝建模技术有以下不足： 1、缺乏高效的物理模型； 一维细长体常见建模方式有弹簧质点模型、弹性杆模型和梁模型，弹簧质点模型 建模易于实施，计算效率高，该方法由一系列质点和连接质点的直线弹簧表示，具有较强的 实时性，但因模型高度简化，准确性低。 利用Kirchhoff理论、Cosserat理论建立的离散弹性杆模型，也可用于模拟介入器 械中导丝运动，Cosserat弹性杆模型利用Cossserat理论，该理论将弹性杆的截面视为刚 体，考虑了弹性杆的轴向线应变和弯曲剪应变等物理参数，以此理论为基础导出杆件的连 续能量表达式，通过对杆的离散计算出杆的每个单元具有的能量，进而由拉格朗日方程得 到杆的动力学微分方程，数值求解该微分方程，得到导丝的动态变化，Cosserat弹性杆模型 能模拟一维细长弹性体任意超大弯曲变形，但杆模型无法考虑导丝的弯曲刚度，同时由于 相连节点之间的变形为小变形，因此要描述柔性体的大变形需划分比较密的网格才能得到 较高精度的解，但其离散之后的导丝中心线为折线。其Kirchhoff弹性杆则是Cosserat弹性 杆模型忽略中心线伸缩及截面截切变形的特例，适用于一维细长弹性体准静力学问题。 相对于杆模型而言，梁模型能考虑导丝的弯曲刚度，针对不同的简化条件，建立 5 CN 111597720 A 说　明　书 2/9 页 Bernoulli梁或Timoshenko梁等不同近似程度的动力学模型，但这两种梁模型应用都基于 小变形假设的前提下，对于导丝的大变形运动，误差显著。 2、碰撞检测； 血管不仅对导丝的运动起到约束作用，当导丝沿血管运动时，其之间还存在移动 接触，为了准确地描述导丝-血管之间接触的力学行为，通常需要将导丝离散成密网格以保 证计算的收敛性。杆/梁-血管接触检测的通常做法是在杆/梁单元内布置接触检测点，看其 是否与管道发生碰撞，AABB(axis-aligned  bounding  box)是一种典型的方法。AABB包围盒 实际上一个长方体检测盒，通过相邻的管道节点构造一系列AABB包围盒，该方法构造简单。 通过对包围盒做循环，确定接触检测点位于哪个包围盒之中，并计算其在血管轴线上的投 影点，该步骤非常耗时，因为必须从血管的顶部到底部依次检查所有的包围盒。最后通过计 算检测点与接触面的相对嵌入深度与速度来计算杆/梁单元所受到的接触力。 因此，开发一种数据处理量小、建模速度快且能够真实模拟导丝的大变形运动的 导丝建模方法极具现实意义。
技术实现要素：
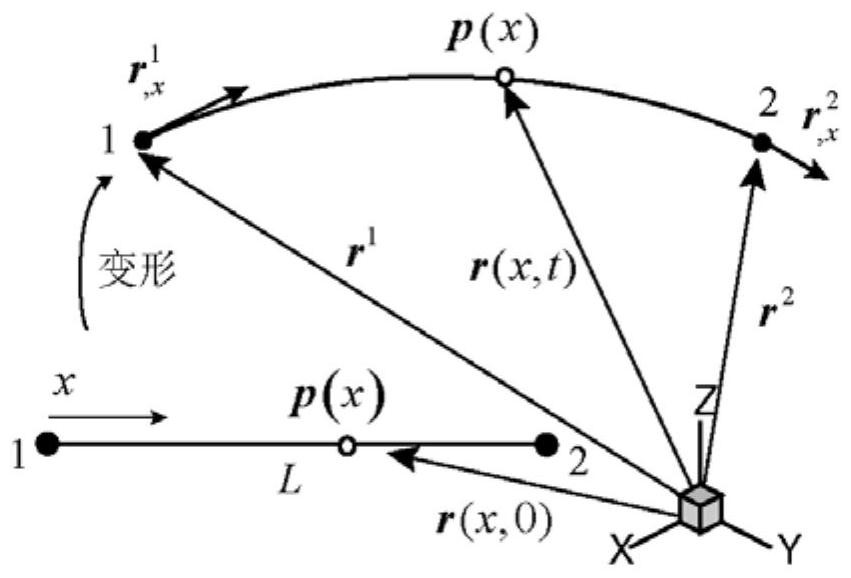
本发明的目的在于克服现有技术无法真实模拟导丝的大变形运动、数据处理量大 且建模速度慢的缺陷，提供一种数据处理量小、建模速度快且能够真实模拟导丝的大变形 运动的导丝建模方法。 为实现上述目的，本发明提供如下技术方案： 一种考虑空间大变形的介入手术导丝建模方法，用于电子设备，步骤如下： (1)将导丝离散成有限个梁单元； (2)单个梁单元以节点位移矢量与位移场的斜率矢量作为广义坐标，通过节点位 移矢量、节点斜率矢量描述导丝变形和导丝截面转动，推导得到单个梁单元的总动能和总 势能的表达式； (3)利用拉格朗日方程将单个梁单元的总动能和总势能以及弹性力结合起来得到 单个梁单元的动力学方程； (4)通过组集所有单元的动力学方程即得整根导丝的动力学方程，所述整根导丝 的动力学方程反映的是整根导丝各作用点所受力的相互关系； (5)结合以下公式与步骤(4)获得的整根导丝的动力学方程即通过导丝一端的位 置信息获取整根导丝所有梁单元的受力及位置信息； δ＝‖r-R‖ rb-rt； 其中，fn为导丝一梁单元与管壁之间的法向接触力，其单位为N，δ、 k、e和c分别 为该梁单元的碰撞侵入深度、相对侵入速度、碰撞刚度系数和碰撞阻尼系数，其单位分别为 mm、mm/s、N/m和N/(mm/s)，e为该梁单元的碰撞侵入指数，其为常数，r、R、rt和rb分别为该梁 单元对应检测点到原点的距离、检测点对应投影点到原点的距离、管道的半径和该梁单元 的半径，其单位分别为mm、mm、mm和mm。 6 CN 111597720 A 说　明　书 3/9 页 本发明采用绝对节点坐标法对导丝柔性体进行建模，首先将研究对象离散成有限 个单元，其中具体是通过推导单元的动能和势能表达式，再结合Lagrange方程建立单元的 动力学方程，而后通过组集所有单元动力学方程得到整个柔性体的动力学方程。本发明基 于绝对节点坐标梁单元理论和拉格朗日乘子式法对导丝建模，由于绝对节点坐标梁单元建 模方法采用了非线性的格林应变来表征应变和变形梯度关系中的几何非线性，对于导丝这 种变形大得足以使结构的位移发生大的变化(即力-位移关系不再是线性关系)的应用场 景，绝对节点坐标梁单元理论的几何非线性描述是精确的，适合描述大位移、大变形运动， 可以直接用来真实地模拟细长弹性体的导丝在手术过程中的曲线运动及引起的弯曲变形。 此外，本发明采用沿管道轴线布置的包围盒代替AABB包围盒进行导丝-血管接触检测，既能 够保证检测所有的接触点，又将接触检测从三维问题简化为一维问题，提高了接触检测的 效率，将联立导丝的动力学方程与导丝-血管碰撞检测方程即可得到整根导丝所有梁单元 的受力及位置间的相互关系，通过获取导丝任一点的位置或受力即可整根导丝所有梁单元 的受力及位置信息。 作为优选的技术方案： 如上所述的一种考虑空间大变形的介入手术导丝建模方法，所述单个梁单元内任 意一点的位置向量r可由梁单元广义坐标e和梁单元形函数N表示，基于绝对节点坐标的梁 单元具体如图1所示； r(X,t)＝N(X)e(t)； 其中，X是单元点上的物质坐标，其单位为mm，t是时间，其单位为s； 单个梁单元内任意一点的绝对位移u可表示为； 其中梁单元节点位移 其单位为mm，e0为梁单元初始构型时的节点广义 坐标。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，所述梁单元广义坐标 e为： e＝[(e1)T  (e2)T]T； 其中梁单元节点的广义坐标包含空间绝对位置向量和其物质导数，每个节点包含 6个广义坐标； 其中，L是梁单元初始构型时的长度，其单位为mm，x∈(0,L)为梁单元物质坐标，其 单位为mm， 是无量纲单位。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，所述梁单元形函数N 为： 7 CN 111597720 A 说　明　书 4/9 页 N＝[N1I  N2I  N3I  N4I]； 其中，N1、N2、N3和N4定义如下： 其 中 ，L 是 梁 单 元 初 始 构 型 时 的 长 度 ，，其 单 位 为 m m ，梁 单 元 参 数 x∈(0,L)为梁单元物质坐标，其单位为mm。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，梁单元的动能Te表达 式为： 其中，ρ是材料密度，其单位为kg/mm3，Me为单元质量阵，V0、和 的单位分别为mm/ s、mm/s和mm/s； 梁单元的应变能U表达式为： 其中，EA和EJ分别为轴向和横向单元刚度，其单位分别为N/mm和N/mm，ε和κ分别为 轴向应变和横向曲率，其均为无量纲单位； 其中， 和 分别为梁曲线的斜率和梁曲线斜率的斜率，其均为无量纲单位。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，单个梁单元的总动能 和总势能分别由梁单元动能和梁单元势能累加而成； 梁单元的总动能TANC和总势能UANC的表达式为： 其中，ei为第i个节点广义坐标向量； 所述弹性能对应的弹性力QK表达式为： 8 CN 111597720 A 说　明　书 5/9 页 利用拉格朗日方程结合TANC、UANC和Qk表达式，得到单个梁单元的动力学方程： 其中，M为系统质量阵，e是系统广义坐标向量，σ为拉氏乘子向量，C(e,t)为约束方 程，Ce为约束方程对广义坐标的求导，Qe为作用在梁单元上的外力，这是一组系统运动微分 方程和代数约束方程集合，通过向后差分法，即backward  differentiation  formulas来求 解这组的微分代数方程。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，通过对血管沿着其母 线进行区间划分，并得到各个区间管道节点的弧长坐标，同时在梁单元中线上内布置接触 检测点，看其是否与管道发生碰撞，因导丝在管道中进行运动，根据梁单元内部的接触检测 点对应的弧长坐标s来确定检测点位于哪个管段内，所需满足的条件为s1≤s≤s2，其中s、 s1和s2分别为接触点以及两个相邻管道节点的弧长坐标，具体如图2所示； 计算接触检测点在管道轴线上投影点的方法如图3所示，梁节点P1、P2分别位于管 道截面s1、s2内，相应的投影点是A1、A2，检测点C1位于单元P1、P2内部，其对应的投影点为 B1，由于B1C1与管道中轴线垂直，B1的弧长坐标s满足 f(s)＝(R-r(s))·r′(s)＝0； 其中R和r分别为检测点C1及其投影点B1到原点的距离，r′为点B1的切向量，上式 是一个非线性方程，可以使用Newton-Raphson方法迭代求解。 如上所述的一种考虑空间大变形的介入手术导丝建模方法，当δ≦0时，fn＝0。 本发明还提供一种电子设备，包括一个或多个处理器、一个或多个存储器及一个 或多个程序； 所述一个或多个程序被存储在所述存储器中，当所述一个或多个程序被所述处理 器执行时，使得所述电子设备执行如上所述的一种考虑空间大变形的介入手术导丝建模方 法。 其中，电子设备具体结构可参考以下描述设计：电子设备内布置有用于实现电气 控制的集成电路板，将其中四个编码器和四个电机与相应的驱动器组合，构成4套直流伺服 驱动单元，各伺服单元之间采用CAN总线通信连接，并经CAN卡，转为USB总线通信，最终与计 算机相连，另外3个编码器与数据采集卡连接，并将数据采集卡将数据传输至计算机； 计算机上安有图形渲染软件，在进行处理时，计算机的CPU(中央处理器)将数据 (包括一些几何体数据(顶点坐标、法向量、纹理坐标、纹理等))加载到显卡(GPU)之中，然后 通过GPU(图形处理器)设置渲染信息，GPU开启渲染，其中顶点坐标变换，光照，剪裁，投影， 屏幕映射都是在GPU中进行。本发明的保护范围并不仅限于此，此处仅给出一种可行的技术 方案而已。 此外，本发明还提供一种计算机储存介质，包括计算机指令，当所述计算机指令在 电子设备上运行时，使得所述电子设备执行如上所述的一种考虑空间大变形的介入手术导 9 CN 111597720 A 说　明　书 6/9 页 丝建模方法。计算机储存介质通过电子设备运行计算机指令时，可进行碰撞检测、碰撞响 应、导丝的物理建模、导丝与血管的渲染、数据的读入，完成血管中导丝的实时运动仿真。 有益效果： (1)本发明的考虑空间大变形的介入手术导丝建模方法，采用绝对节点坐标梁单 元理论参与建模，其采用了非线性的格林应变来表征应变和变形梯度关系中的几何非线 性，适合描述大位移、大变形运动，可直接用来真实地模拟细长弹性体的导丝在手术过程中 的曲线运动及引起的弯曲变形； (2)本发明的考虑空间大变形的介入手术导丝建模方法，采用沿管道轴线布置的 包围盒代替AABB包围盒进行梁-管道接触检测，既能够保证检测所有的接触点，又将接触检 测从三维问题简化为一维问题，极大地减少了数据处理量，提高了接触检测的效率； (3)本发明的电子设备，结构简单，成本低廉，能够快速精确地进行介入手术导丝 建模，应用前景好。 附图说明 图1为本发明的单个梁单元的示意图； 图2为本发明的梁的接触检测算法的示意图； 图3为本发明的计算接触检测点在管道轴线上投影点的示意图； 图4为本发明的一种考虑空间大变形的介入手术导丝建模方法的流程图； 图5为本发明的电子设备的结构示意图； 图6为本发明的电子设备的处理逻辑示意图。