技术摘要：
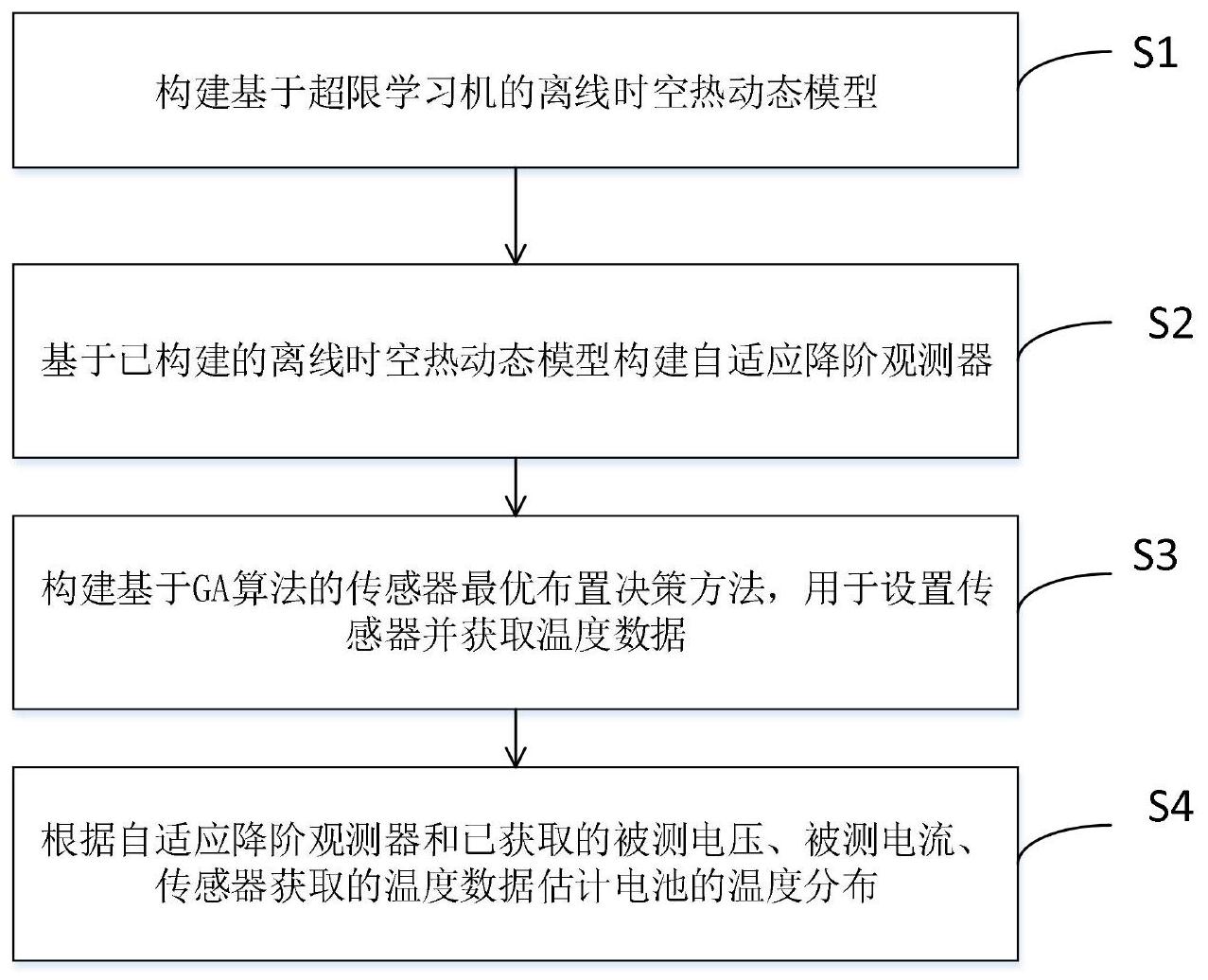
本发明公开了一种基于降阶模型的锂离子电池在线温度分布观测器设计方法，包括以下步骤：S1：构建基于超限学习机的离线时空热动态模型；S2：基于已构建的离线时空热动态模型构建自适应降阶观测器；S3：构建基于GA算法的传感器最优布置决策方法，用于设置传感器并获取温  全部
背景技术：
随着油价飙升和气候变化问题的日益严重，石油消费引起的能源和环境问题已成 为当今时代的一大挑战[1]。为了解决这一问题，新能源得到了迅速发展[2]。锂离子电池 (LIBs)以其能量密度高、比能量高、环境污染低等优点，被广泛应用于电动汽车(EVs)和混 合电动汽车(HEVs)的动力源中[3-5]。由于电池的寿命、效率和安全性都取决于电池的热性 能，因此，精确的电池热管理系统(BTMS)对于保证电池工作在最佳温度范围内是必不可少 的[6-8]。 电池内部的热过程是一种典型的分布式参数系统(DPS)，通常采用复杂的非线性 偏微分方程(PDEs)来进行描述[9-11]。DPS的输入、输出甚至状态参数都会在时间和空间上变 化[12-13]。然而，在实际的BTMS中，只有有限的传感器可以用于在线温度测量。因此，需要建 立一个可在线使用和更新的精确数学模型，对温度分布进行在线监测。在LIBs热模型的开 发方面，已有大量的研究报道，主要分为集总热模型和分布式热模型两大类。 现有方案及存在的问题及缺点： 集总热模型假设电池内部温度分布均匀。也就是说，温度只是时间的函数[14-15]。 由于这种模型的简单性，它们被广泛地用于表征电池的热行为。集总模型与电化学模型相 结合[16-17]或等效电路电模型[18-20]的研究，已经成功地应用于电池或圆柱电池。这些模型对 于温度控制和BTMS设计来说是非常简单的。然而，他们没有考虑电池空间的温差[21]。为了 更准确地监测和预测温度，需要分布式热模型来解释温度在时间和空间上的变化。近年来， 人们研究了各种表征LIBs热行为的分布模型[22-24]。与集总模型一样，大多数分布式热模型 都与电化学模型耦合，从而解释了热的产生。上述模型可以为电池设计提供非常准确的信 息。然而，它们不适用于高计算负荷的在线温度监测和控制等相关应用[25]。为了建立面向 BTMS应用的降阶模型，研究者已经做了一些工作。在文献[26]中，采用适当的正交分解(POD) 方法，也称为Karhunen-Loève(KL)方法，建立了锂离子电池的还原电化学热模型。在文 献[27]中，基于Laplace变换，建立了柱状棱柱型锂离子电池的降阶热模型。拉普拉斯变换方 法仅适用于线性模型，不能有效地模拟非线性电池热动态。在的文献[28]中，提出了一种基 于KL的二维电池热过程时/空分离方法。 虽然这些模型对于在线应用来说很简单，但挑战仍然存在，因为电池的行为会随 着时间的推移和不同的工作环境而改变。这些时变动态行为可能是由化学模型参数的老 化、工作条件的变化和外部扰动引起的[5]。为了进行准确可靠的热管理，应设计先进的辨识 和估计方法，使所开发的模型能够适应时变环境[29]。然而，在大多数这些模型中，没有认真 考虑温度分布。在文献[30]中已开发了一种用于在线估计圆柱形柱LIBs温度的参数化方案。 5 CN 111595485 A 说　明　书 2/12 页 它们的参数用递归最小二乘法自动识别。然而，由于电池的时空分布较强，仅用两种集总模 型分别近似车用电池的核心温度和表面温度，不可能适用于大型汽车电池。 基于时间/空间分离的建模方法已经被广泛地应用于锂离子电池(LIB)热动态的 估算。然而，这些方法是在离线环境下发展起来的，在实时应用中可能表现不好，因为电动 汽车(EVs)的电池系统通常会受到外界的干扰。此外，温度车载测量常常受到大误差的影 响。
技术实现要素：
本发明为克服上述现有技术的锂离子电池在线温度检测效果不理想的缺陷，提供 一种基于降阶模型的锂离子电池在线温度分布观测器设计方法。 本发明的首要目的是为解决上述技术问题，本发明的技术方案如下： 一种基于降阶模型的锂离子电池在线温度分布观测器设计方法，包括以下步骤： S1：构建基于超限学习机的离线时空热动态模型； S2：基于已构建的离线时空热动态模型构建自适应降阶观测器； S3：构建基于GA算法的传感器最优布置决策方法，用于设置传感器并获取温度数 据； S4：根据自适应降阶观测器和已获取的被测电压、被测电流、传感器获取的温度数 据估计电池的温度分布。 本方案中，构建基于超限学习机的离线时空热动态模型的具体步骤包括： 采用Karhunen-Loève方法计算最优空间基函数，并通过最优空间基函数进行时空 分解， 利用得到的最优空间基函数用Galerkin方法推导出降级模型的数学表达式，再利 用ELM算法辨识未知结构和参数； 利用时间/空间重构离线时空模型； 具体过程为： 将时空变量T(x,y,t)展开为时间/空间解耦形式，如下： 其中 是空间基函数，ai(t)是对应的低阶时间模型，n是模型阶数； 使用Karhunen-Loève方法的KL分解来估计 下一个阶段是识别时间模型ai (t)的表达式，具体如下： 将式(1)替换为基于物理的模型，方程差表示为： 其中，k0、k1、k2为常数，表示不同方向的热导率； 采用Galerkin方法，ai(t)的离散形式表示为： 其中kij和 是常数，然后式(3)用离散形式描述为： 6 CN 111595485 A 说　明　书 3/12 页 a(k)＝K1a(k-1) K2q(k-1)   (4) T(x,y,k)＝Ca(k)      (5) 其中，a(k)＝[a1(k) ,...,a Tn(k)] ,K1＝{kij}n×n , q(k)＝[q1 (k) ,...,qn(k)]T, K1、K2表示常数，C是空间基函数组； 采用单隐层前馈神经(SLFN)网络来近似公式(4)中的未知非线性函数q(k)；然后 公式(4)中的a(k)表示如下： 其中N是SLFN网络的隐神经元数，βp是连接相应隐神经元和网络输出神经元的输 出权重，ωp是连接相应隐神经元和输入神经元的输入权重，ηp是相应隐神经元的阈值，G (·)是隐神经元的激活函数z(k)＝[I(k)，V(k)]T 获得与时空测量{T(x,y,k)}相对应的时间系数a(k)的值，计算公式如下： 方程(4)中的模型参数就可以用一组数据 来识别；模型(6)用线性回归 形式写为： a(k)＝H(k-1)θ     (8) 其中，H(k-1)＝[a(k-1) ,G(ω1·z(k-1) η1) ,...,G(ωN·z(k-1) ηN)],θ＝[K1,K2 β1 ,...,K2βN]T是要估计的参数向量，引入ELM算法来识别式(8)中存在的未知参数，对于 ELM，ωp和ηp都是随机生成的，与训练数据无关； 等式(6)能够以矩阵形式表示为： a＝Hθ     (9) 计算出参数θ如下： 其中 是矩阵H的Moore-Penrose广义逆矩阵，降阶模型式(6)训练完毕之后，利用 时间/空间合成形式重构电池热过程的离线时空热动态模型。 本方案中，步骤S2自适应降阶观测器的构建过程为： 利用估计温度与在线测量温度之间误差的反馈，根据识别出的降阶模型来设计观 测器，表达式如下： 其中，Tm是在线测量温度，m是在线测量的数量，m＜＜M和M＝nx×ny是用于模型识 别的离线测量的数量； 是用估计的 重构的温度场，L是观测器的增益矩阵，在 趋 近于a(k)时确定率，即 Cm的形式如下： 7 CN 111595485 A 说　明　书 4/12 页 Cm是空间基函数矩阵； 观测器的性能与增益矩阵L和传感器m的位置高度相关，将传感器位置m的选择与 在线温度分布估计观测器的设计相结合，找出符合条件的m和L值，从而最小化下列目标函 数 使服从: 其中，Q是正定加权矩阵， 表示估计的温度场。 本方案中，自适应降阶观测器的设计还包括： 根据已建立的ELM低阶模型，将自适应降阶观测器设计为： 其中，g(k)＝[g1(k) ,g2(k) ,...,gn(k)]T, 选择增益L保证K1-LCm是稳定的，g(k)是隐神经元的激活函数矩阵、gi( )是隐神经元的激活 函数和。 本方案中，构建基于GA算法的传感器最优布置决策方法具体步骤为： 步骤1：种群初始化：生成由n个个体组成的随机种群；所述个体为传感器； 步骤2：适应度计算：用成本函数 评估每个个体的适应度； 步骤3：生成新的种群：通过重复以下过程创建新的群体： 选择：根据适应度值选择交叉的父代个体：保留最佳适应度的个体，并用它来替换 掉最差个体；使用轮盘赌选择法选择其它个体； 交叉：从父代中随机选择的两个个体，将以一定的交叉概率交叉，以产生下一代； 变异：为了保持传感器的数量，随机选择的nd个元素将发生变异，nd表示新一代中 传感器的数量(在个体中表示为1)和预先设计用于在线估计的传感器m的数目之间的差； 步骤4：重复步骤2和步骤3，直到满足停止条件为止。 本方案中，在实施GA算法时，设定在线测量传感器的数量是固定的。 与现有技术相比，本发明技术方案的有益效果是： 本发明通过构建基于超限学习机的离线时空热动态模型结合自适应降阶观测器 和基于GA算法的传感器最优布置策略，观测器的性能得以提高，同时提高了在线温度检测 效果。 8 CN 111595485 A 说　明　书 5/12 页 附图说明 图1为本发明方法流程图。 图2为基于GA的最优传感器布置决策方法流程图。 图3为模型识别的输入信号及测量电压示意图。 图4为模型标识在不同时间的温度分布图。 图5为使用不同时间的训练数据的基于ELM的时空模型的预测误差示意图。 图6为用于在线估计的传感器位置优化示意图。 图7为模型验证在不同时间的温度分布图。 图8为在不同时间对测试数据，进行传感器位置优化的，所提模型预测误差示意 图。 图9为平均分布式传感器模型对不同时刻测试数据的预测误差示意图。 图10为观测器性能比较的点1处的温度变化示意图。 图11为观测器性能比较的点2处的温度变化示意图。 图12为TNAE方面的性能比较示意图。