技术摘要：
本发明公开了一种考虑表面完整性的疲劳寿命预测方法，应用于疲劳寿命及可靠性领域，为解决航空发动机零部件在考虑表面完整性时的疲劳寿命预测问题。本发明结合经典的疲劳寿命模型，引入表面完整性参数对寿命模型进行修正，首先开展光滑无应力试样的疲劳试验，获得材料  全部
背景技术：
航空发动机关键零部件的疲劳性能与其表面完整性直接相关，而表面完整性参数 如表面粗糙度和残余应力显著影响零部件疲劳性能。实际零部件的疲劳裂纹通常在表面缺 陷处和应力集中区域萌生，已有的研究表明，表面形貌、表层残余应力和微观组织结构对疲 劳寿命有重要影响，表面粗糙度越小，表面残余压应力越大和表面硬度越高，零部件疲劳寿 命越长。然而，当采用某些特定的制造参量的组合加工时，其结果并不能保证这些表面完整 性参数均达到最优。如何根据构件的具体服役条件实施更加有效的抗疲劳制造，则需要借 助理论研究，确定表面完整性参数对材料疲劳寿命模型的影响，以实现对于航空发动机零 部件寿命的准确预测。
技术实现要素：
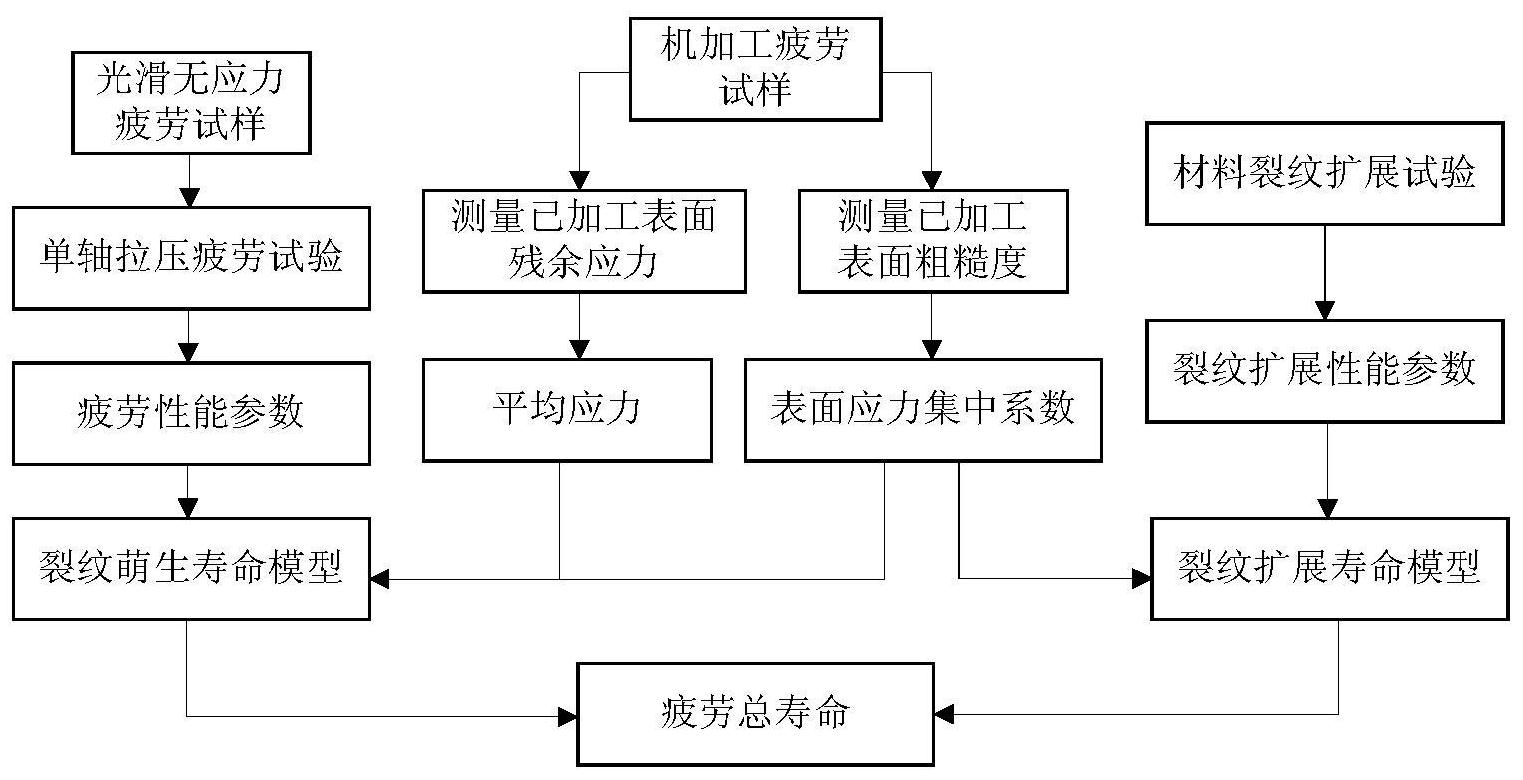
本发明的目的在于，克服现有技术存在的技术缺陷，提出一种考虑表面完整性的 疲劳寿命预测方法，解决表面完整性参数影响零部件疲劳寿命的问题。 本发明具体采用如下技术方案：一种考虑表面完整性的疲劳寿命预测方法，其特 征在于，包括如下步骤： 步骤一：参考GB/T  15248-2008设计疲劳试样尺寸，对机加工后疲劳试样的标距段 进行表面打磨和抛光处理获得光滑无应力试样，对于打磨抛光后的光滑无应力试样开展单 轴拉压疲劳试验，获得疲劳性能参数； 步骤二：参考GB/T  15248-2008设计疲劳试样尺寸，采用给定的切削参数(如切削 速度、进给量和背吃刀量)切削加工疲劳试样，采用粗糙度轮廓仪测量疲劳试样标距段的已 加工表面粗糙度Ra和Rz，采用X射线衍射测量疲劳试样标距段已加工表面沿轴向的残余应力 σaxial； 步骤三：对测量完表面完整性参数的疲劳试样开展单轴疲劳试验； 步骤四：将疲劳试样标距段已加工的表面轮廓视为微观缺口，计算微观缺口处的 应力集中系数Kt； 步骤五：将疲劳试样标距段已加工表面的应力集中系数Kt和沿轴向残余应力σaxial 引入Basquin应力幅—寿命模型，计算裂纹萌生寿命Ni； 步骤六：计算疲劳试样标距段已加工表面微观缺口处产生初始裂纹时的应力强度 因子K； 步骤七：将疲劳试样标距段已加工表面的应力集中系数Kt，以及疲劳加载中应力 比R引入Paris公式，计算裂纹扩展寿命Np； 步骤八：将步骤五和步骤七中分别计算得到的裂纹萌生寿命Ni和裂纹扩展寿命Np 6 CN 111553091 A 说　明　书 2/8 页 相加，则得到考虑表面完整性的疲劳总寿命，即有Nf＝Ni Np。 作为一种较佳的实施例，所述步骤一中的所述表面打磨和抛光处理的工艺为：采 用800#至2000#水磨砂纸沿平行和垂直于疲劳试样的轴向进行打磨，随后采用抛光布和W1 抛光剂进行抛光处理，打磨和抛光后疲劳试样表面粗糙度Ra≤0.2μm，疲劳试样表面视为无 残余应力。 作为一种较佳的实施例，所述步骤一中的所述单轴拉压疲劳试验的疲劳试验条件 为：试验温度为室温；采用应变控制，应变比Rε＝-1；加载波形为正弦波，加载频率Nf为0.5Hz ～1.0Hz；通过应变引伸计读取疲劳试样的应变值。 作为一种较佳的实施例，所述步骤一中的所述疲劳性能参数如以下Manson- Coffin寿命方程所示： 其中，σ'f为疲劳强度系数；ε'f为疲劳延性系数；Nf为加载频率；b和c分别为疲劳强 度指数和疲劳延性指数，通过疲劳试验数据拟合获得。 作为一种较佳的实施例，所述步骤三中的所述单轴疲劳试验的疲劳试验条件为： 试验环境温度为室温；加载波形为正弦波，加载频率为1Hz；采用应力控制，疲劳交变应力最 大值选择低于材料的屈服应力，应力比R＝-1。 作为一种较佳的实施例，所述步骤四具体包括：微观缺口处的应力集中系数Kt计 算公式为： 其中，γ＝b/t，b为缺口间距，t为缺口深度，ρ为缺口根部曲率半径，Rz为表面粗糙 度参数：微观不平度十点高度；n是与缺口处应力状态相关的系数，n＝1时代表剪切状态，n ＝2时代表拉伸状态。 作为一种较佳的实施例，所述步骤五中的所述寿命模型的计算过程为：将疲劳试 样标距段的已加工表面残余应力视为在疲劳加载中的平均应力σm，即σm＝σliax，同时考虑表 面应力集中系数，则将Basquin应力幅—寿命关系修正为： Ktσa＝(σ′f-σ bm)·(2Ni) ； 上式中的疲劳性能参数由所述步骤一中得到。 作为一种较佳的实施例，所述步骤六中的所述应力强度因子K采用下式计算： 式中，σt为拉伸应力，Q为椭圆积分，Fs为表面裂纹的几何修正函数，a，c，t和b分别 为裂纹宽度，裂纹半长，有限体宽度和有限体半长；φ为裂纹扩展处角度。 作为一种较佳的实施例，所述椭圆积分Q计算公式如下： 7 CN 111553091 A 说　明　书 3/8 页 所述几何修正函数Fs采用下式计算： 上式中各项系数计算方式如下： 作为一种较佳的实施例，所述步骤七中的所述裂纹扩展寿命Np计算步骤如下： 首先考虑疲劳试样的已加工表面应力集中系数Kt，和疲劳试验中应力R比对裂纹 扩展寿命的影响，定义有效应力强度因子幅度ΔKeff为： 8 CN 111553091 A 说　明　书 4/8 页 ΔKeff＝UKtΔK＝UKt(Kmax-Kmin)； 式中应力集中系数Kt由所述步骤五中计算得到，应力强度因子K的最大值Kmax和最 小值Kmin由所述步骤七中计算得到；U为裂纹闭合参数，定义U与应力比R具有如下关系： U＝0.55 (0.45-α)R αR2； 式中α为基于材料试验数据的拟合参数；采用描述材料稳定扩展的Paris公式描述 材料裂纹扩展寿命，则裂纹尺寸a与疲劳寿命N具有如下关系： 裂纹扩展性能参数C和m由材料裂纹扩展试验获得；对上式积分得到裂纹扩展寿命 Np计算公式如下： 上式中a0为初始裂纹尺寸，取工程目视可见裂纹尺寸，ac为临界裂纹尺寸，由下式 计算获得： 上式中KIC为材料I型断裂韧性。 本发明所达到的有益效果：第一，本发明针对如何根据构件的具体服役条件实施 更加有效的抗疲劳制造，确定表面完整性参数对材料疲劳寿命模型的影响，以实现对于航 空发动机零部件寿命的准确预测的技术需求，本发明以成熟的疲劳寿命预测模型为基础， 引入表面完整性参数对其进行修正，模型物理意义明确，具有较强的理论支撑。第二，本发 明同时考虑了裂纹萌生寿命和裂纹扩展寿命，明确了表面完整性参数对裂纹萌生寿命和裂 纹扩展寿命的影响，深化了零部件表面状态对疲劳寿命的理解。第三，本发明将已加工表面 视为微观缺口，采用应力集中系数描述缺口处应力集中程度，提高了寿命预测的精度。 附图说明 图1是本发明的一种考虑表面完整性的疲劳寿命预测方法的流程图； 图2是GH4169镍基高温合金单轴拉压疲劳试件尺寸示意图，单位为mm； 图3是采用本发明对GH4169镍基高温合金的预测疲劳与试验寿命比较图。