技术摘要：
本发明公开了属于电力系统建模及稳定性分析领域的一种基于模态频率处电气阻尼的次同步谐振风险量化评估方法，首先针对实际的火电机组接入复杂电网系统，建立相应的网络空间模型，通过其得到对应的网络参数矩阵，并与被研究的发电机组状态空间方程联立，建立整个系统的  全部
背景技术：
我国煤炭资源丰富，但地理分布极不均匀，呈现“南多北少”、“西少东多”的能源分 布特征；同时，除东南沿海地区的风能资源外，我国的水资源和风能资源也均集中分布在西 南等地。然而，经济中心与电力负荷中心分布在我国中部与东南沿海地区，因此能源分布与 负荷呈现逆向分布的特点，也就决定了“西电东送”的基本格局与发展战略。早期，我国就出 现了次同步振荡问题，大多集中于大型火电机组与串补输电线路之间，如我国的锦界电厂、 托克托电厂、上都电厂、伊敏一、二期电厂等。目前虽然已有对串补导致次同步谐振的解决 方案，但基本都处于对单机(规模不大)，点对网直接由串补送出的系统。近几年来，我国特 高压线路越来越多，系统也变得越来越复杂，串补送出系统不再呈现点对网的单一模型，因 此，当系统结构发生变化时，整个系统的谐振频率可能会产生较大的变化，这对串补引起的 次同步谐振有很大的影响，仅由经验判断并不能全面分析整个系统的风险程度，研究人员 即使通过时域仿真来评估风险也存在弊端，系统的运行方式组合数成千上万时，这将具有 很大的工作量，难以一一仿真实现，因此需要一种批量且量化处理次同步谐振风险评估的 方法。 本发明以复转矩系数法为基础，通过形成系统状态空间方程，利用电网电气谐振 模式与串补产生电气谐振频率之间的关系，提出了一种针对火电机组接入含串补复杂交流 电网的基于模态频率处电气阻尼的次同步谐振风险量化评估方法，该方法可以通过编程实 现，大大简化了研究人员的工作量，并且能够全面、高效、准确的量化评估次同步谐振风险， 能够满足实际工程中对电力系统次同步谐振特性分析的要求。
技术实现要素：
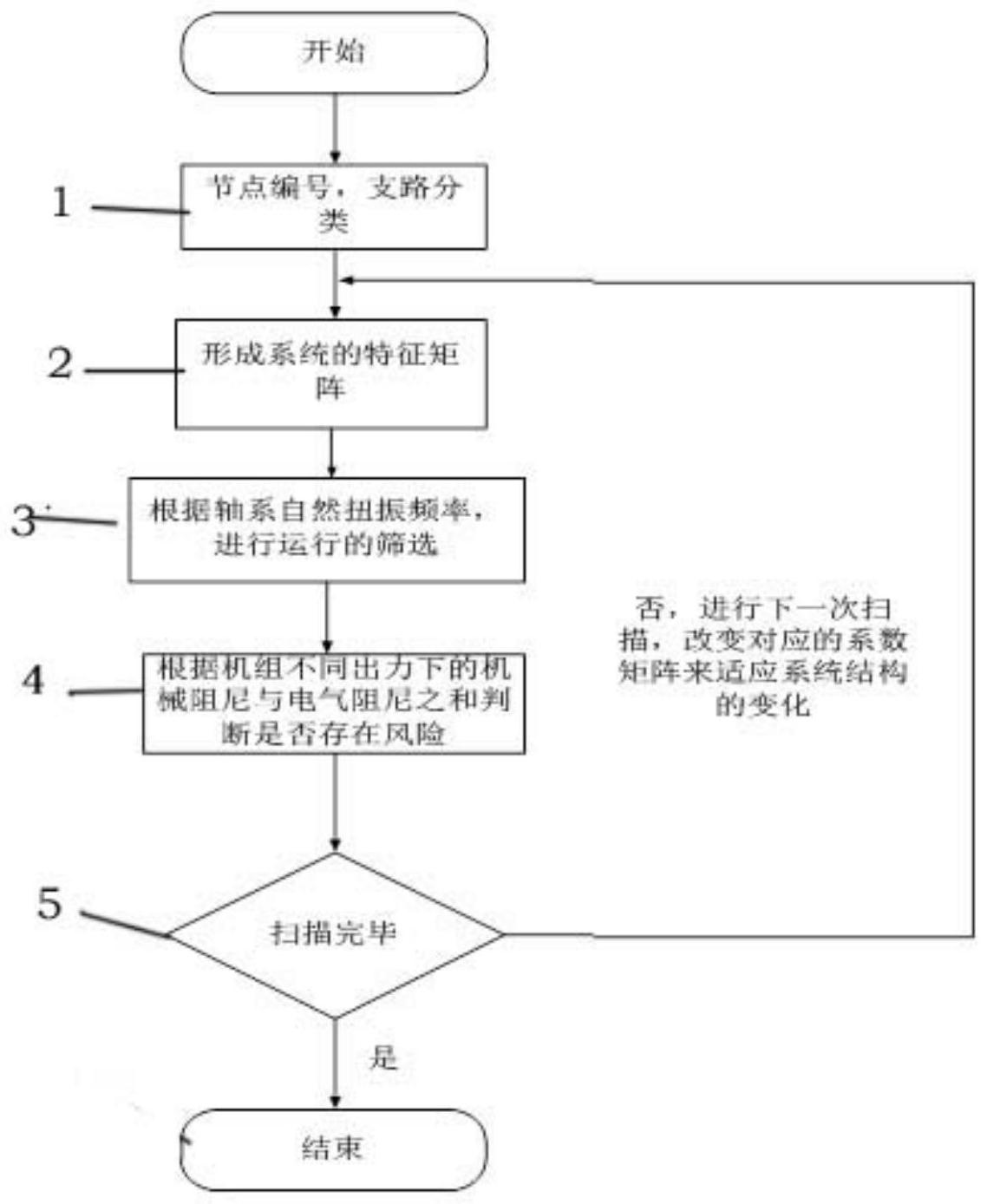
本发明的目的是提出一种基于模态频率处电气阻尼的次同步谐振风险量化评估 方法，其特征在于，该方法是一种火力同步发电机组接入含串补复杂交流电网的基于模态 频率处电气阻尼的次同步谐振风险量化评估方法，包括如下步骤： 步骤1：针对火电机组接入复杂电网系统，建立网络模型，对节点编号，并对不同的 支路、节点类型分为等值电源节点、电容支路及阻感支路三种类型； 步骤2：通过网络模型得到对应的Y1、Y2、L1、L2、Le1、Le2、BL、BG、Be、AL、AG、Ae的网络参 数矩阵，通过与被研究发电机组的状态空间方程联立，建立整个系统的状态空间方程； 步骤3：初步筛选出由串补电容引起的次同步谐振频率，保留与待研究机组轴系自 然扭振模态频率相近的工况； 步骤4：计算发电机组轴系自然扭振模态频率处的电气阻尼值，与机械阻尼进行比 6 CN 111597680 A 说　明　书 2/9 页 较，通过判断机械阻尼与电气阻尼之和的正负来判断是否存在次同步谐振特性，实现批量 处理发电机组接入复杂大电网的次同步谐振风险量化评估； 步骤5：根据电厂的实际情况与整个接入电网的运行方式为基础，再一次对步骤4 中的工况进行筛选，得到电厂机组实际运行中存在风险的工况。 所述步骤2中通过网络模型得到对应的Y1、Y2、L1、L2、Le1、Le2、BL、BG、Be、AL、AG、Ae的网 络参数矩阵，用类似节点导纳矩阵的构成方法建立发电机组的状态空间方程包括： 所述电容支路： 所述阻感支路： 上式(1)、(2)中的x、y代表整个网络方程建立的同步坐标系；c、R、L代表对应支路 电容值、电阻值以及电感的大小，ωB＝100π，p为微分算子d/dt； 其中，所有电容支路对应其节点并以y1为元素构成矩阵Y1，同理所有电容支路对应 其节点并以y2为元素构成矩阵Y2；所有输电线路以及负荷支路对应节点并以l1为对角线元 素构成L1，所有输电线路以及负荷支路对应节点并以l2为对角线元素构成L1；由等值电源所 在支路对应其节点并以l1为对角线元素构成Le1,由等值电源所在支路对应其节点并以l2为 对角线元素构成Le2；BL、BG、Be分别以各电容支路节点相关，流入为正(1)，流出为负(-1)，构 成对应的矩阵；AL、AG、Ae与其支路对应的节点电压相关，同样流入为正(1)，流出为负(-1)， 构成对应的矩阵。 通过上面的矩阵构成原则，可以得到发电机外网络部分的状态方程： pΔu＝-Y -1Y Δu Y -1B Δi Y -1 -11 2 1 L L 1 BeΔie Y1 BGΔiGxy    (3) 上式中的u为网络中与电容有关的节点电压列向量，iL为输电线路或者阻感负载 的电流列向量，ie为等值电源的电流列向量，iGxy为发电机端xy坐标系下的电流列向量； 通过发电机外网络部分的状态方程建立的发电机的状态空间方程： pΔiG＝X1ΔiG X2ΔwG X3ΔuGdq    (6) 式(4)中，iG为发电机的状态变量，ωG为发电机的转速，uGdq为发电机的机端电压， X1、X2、X3为发电机状态空间方程的系数矩阵。 所述考虑坐标变换，将网络中的状态方程统一到被研究机组的dq轴上。 7 CN 111597680 A 说　明　书 3/9 页 F为对应的电压或者电流向量，δT为绝对公角，即同步坐标系x轴与发电机q轴之间 的角度。 通过联立式(3)、(4)、(5)、(6)、(7)，可以得到整个系统的空间状态方程： pΔX＝AΔX BΔωG    (8) X为状态变量，包括与电容支路节点相关的节点电压Δu，输电线路或者阻感负载 的电流ΔiL，等值电源的电流Δie，发电机的对应的状态变量ΔiG以及被研究发电机的转子 角ΔδG，A为状态方程的特征矩阵，B为输入矩阵。 以被研究的发电机的转矩输出量ΔTe作为整个状态方程的输出： 上式中，Ψq0、Ψd0、id0、id0为发电机的磁链、电流初始值，xd、xad、xdq、xd为发电机的 电气参数，C为输出变量ΔTe与状态变量ΔX之间的关系。 所述电气阻尼的次同步谐振风险，通过(8)、(9)可以很容易得到整个系统的输入 输出之间的关系式(10)，并得到系统电气部分的电气阻尼表达式(11)。 通过状态方程的特征矩阵A，快速得到整个系统电气部分的振荡模式，考虑到火电 机组经串补送出的复杂系统网络中，串补电容是导致电气阻尼呈现负值的原因，因此需要 将与串补电容有关的特征值筛选出来，由串补电容引起的特征值都具有一个相同的特征， 即在所有的特征值中存在两个以2倍工频(100Hz)互补的特征值，以此为筛选原则，得到仅 由串补引起的特征值，(筛选流程图如图2所示) 其中分别设5～48Hz的频率分量为f1,52～95Hz的频率分量为f2,该频率门槛的设 置是以实际为标准，通过判断式 f1_p f2_q＝100Hz，p＝1,...,g；q＝1,...,z    (12) 上式中f1_p和f2_q分别对应于不同的工况下，位于两个频段中的频率，g、z即对应该 频段频率的个数，若满足式(12)，则保留该频率，根据式(13)进行下一步判断。 |f1_p-fwr_i|≤1,p＝1,...,g；i＝1,...,s    (13) fwr_i对应于待研究发电机组的轴系自然扭振模态频率，s对应于轴系自然扭振频 率的个数，对于满足式(13)的频率及对应的工况进行保留，若不满足，则直接进行下一次工 况的扫描。 所述计算发电机组轴系自然扭振模态频率处的电气阻尼值，通过判断模态频率处 电气阻尼与机械阻尼之和的正负来判断是否存在次同步谐振发散现象； 8 CN 111597680 A 说　明　书 4/9 页 1)根据式(11)计算电气阻尼值 设发电机组轴系自然扭振模态频率为ω(m)，代入式(11)，计算得到发电机组轴系 自然扭振模态频率处的电气阻尼值： 2)机械阻尼的计算 机组轴系分段集中质块-弹簧模型的数学表达为 δ为电气扭角向量,ω为电气角速度,ΔT为机械转矩与电磁转矩的差值,M为转动 惯量矩阵,K为弹性系数矩阵,D为阻尼系数矩阵； 将式(15)进行解耦后，即在方程两边同乘PT,P满足P-1M-1KP为对角矩阵，得到，并令 δ＝Pδ(m)，即可得到解耦后的表达式： 上标(m)表示解耦后的量，将电气阻尼考虑到式(16)中，可以得到： PNk表示P矩阵中第N行k列的元素，其中N为发电机位于第N个质块的位置，k对应于 相应的轴系频率。即可以通过判断 的正负来判断系统是否稳定，并且可以通过 值的大小来得到对应整个系统特征值的大小，机组出力改变时，即可通过改 变D(m)的大小来得到不同的结果，保留不同工况下 为负的情况。 根据电厂发电机组的实际情况与整个接入电网的运行方式为基础，再一次对步骤 4中的工况进行筛选，得到电厂机组实际运行中存在风险的工况，实现了对机组次同步谐振 风险运行工况的量化评估。 本发明的有益效果是根据电厂的实际情况与整个接入电网的运行方式为基础，多 次对电厂的实际工况进行筛选，得到电厂机组实际运行中存在风险的工况。得到了机组不 同出力、不同运行方式下的存在次同步振荡的工况，针对其中可能存在一些实际系统中本 身就不允许出现的运行方式，设定如特高压变的最高允许退出的台数、临近发电机组的投 退台数等一些约束条件：对人为的并且对一些过于极端的运行方式剔除；或可以直接画出 整个频段的电气阻尼曲线，并结合时域仿真来更全面观察其风险程度，从而可以避免来回 使用测试信号法来获得电气阻尼曲线，大大减少了工作量和时间。 附图说明 图1次同步谐振风险量化评估方法流程图。 9 CN 111597680 A 说　明　书 5/9 页 图2为发电机组接入复杂网络的系统结构图 图3为电气阻尼对比曲线图 图4  26.5Hz模态分量曲线图 图5为电网结构系统示意图