技术摘要：
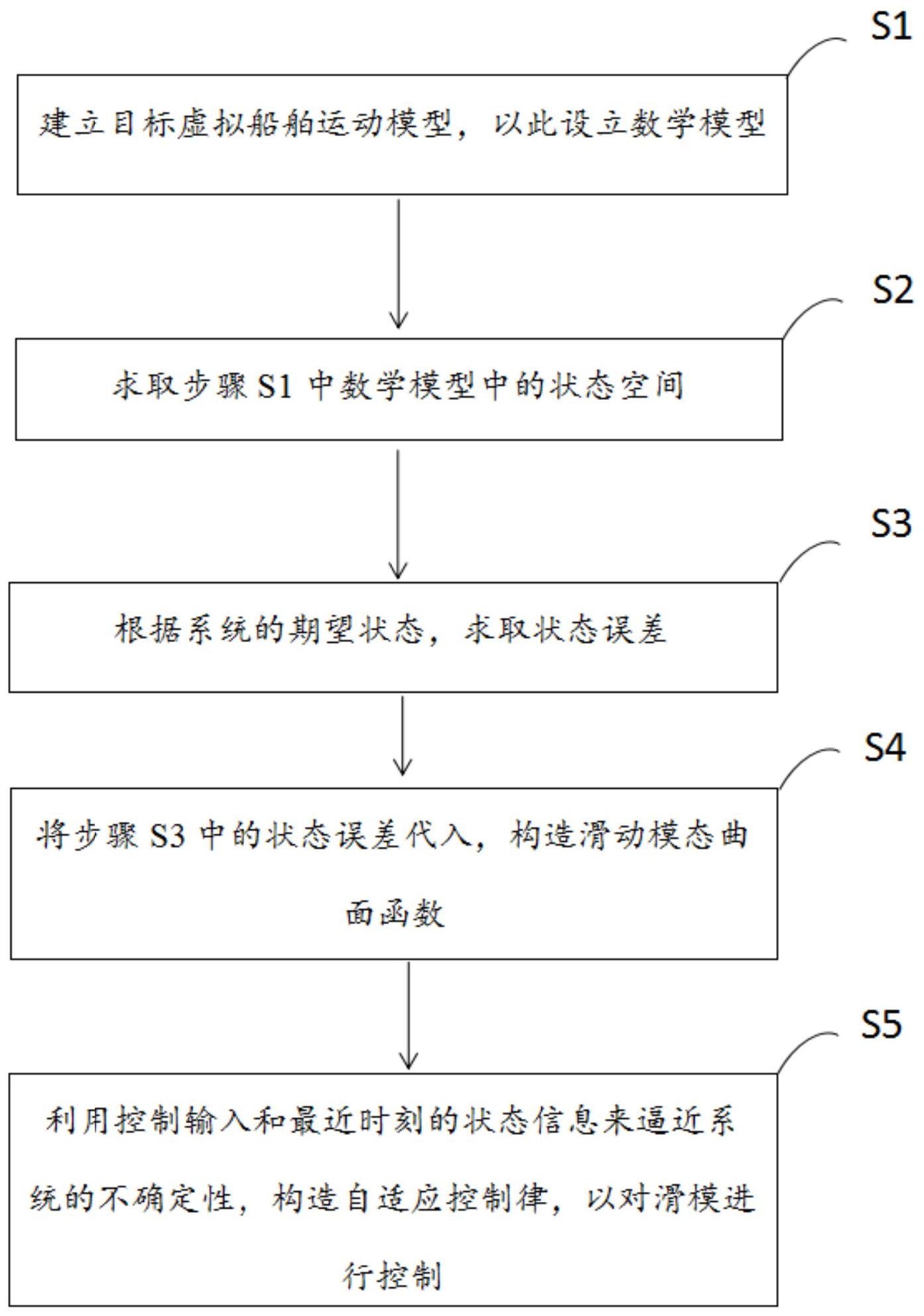
本发明公开了一种基于时滞分数阶船舶运动自适应滑模控制方法，所述控制方法包括以下步骤：S1，建立目标虚拟船舶运动模型，以此设立数学模型；S2，求取步骤S1中数学模型中的状态空间；S3，根据系统的期望状态，求取状态误差；S4，将步骤S3中的状态误差代入，构造滑动模  全部
背景技术：
随着世界航运业的迅速发展，船舶航行安全以及现代化程度要求越来越高，因此 船舶航行控制受到了广泛的关注。近几十年，出现了各种用于船舶控制系统的先进控制算 法，如鲁棒控制、自适应控制以及各种智能控制方法等。但大多控制方法并没有应用于实际 的控制系统中，一方面由于高级的控制方法带来了控制器设计上的复杂性以及过重的计算 负担，另一方面与船舶运动的高度非线性以及复杂的海况也有很大关系。 目前，船舶定位设备主要采用PID控制、线性二次型最优控制、  backstepping积分 控制、模糊控制和混合切换控制[1-5]。滑模控制是20世纪50年代苏联学者提出的变结构控制 的一个分支，属于通过切换函数实现的非线性控制。根据系统状态的偏差程度，将控制律 (或控制器参数)从滑模变为滑模。它对参数变化不敏感，具有抗干扰能力。近年来，滑模控 制在船舶动力定位领域得到了迅速的发展。针对自主式水下机器人(auv)，王建民提出了一 种基于backstepping方法、自适应神经网络和动态表面控制技术的鲁棒滑模编队控制策 略[6]。Zhang提出了一种基于自适应不确定性补偿的自适应终端滑模控制方法，实现了水下 机械手遥操作系统参考位置的主位置跟踪[7]。提出了一种基于径向基函数神经网络 (RBFNN)局部逼近的从动机械臂位置跟踪方法。采用基于Ge-Lee(GL)矩阵的RBFNN直接逼近 从机械臂动力学的各个单元，并设计了具有适当更新规律的鲁棒项来抑制估计模型与实际 模型之间的误差和外界干扰。邵为船舶三自由度运动模型设计了滑模控制器和自适应滑模 控制器[8]。DAI提出了一种基于强化学习的自适应迭代滑模控制方法，用于欠驱动船舶的路 径跟踪[9]。秦采用了终端滑模和自抗扰控制方法[10]。王提出了终端滑模控制方法和辅助线 性滑模面[11]。 针对不确定时滞系统设计鲁棒控制器已成为一个关键问题。滑模变结构控制的鲁 棒性使其对模型误差、参数变化和外界干扰不敏感。因此，变结构控制已成为时滞系统的一 种有效控制方法。随着变结构控制理论的发展，对时滞系统的变结构控制进行了一些研究 。[12-13]Roy提出了一种针对参数不确定性的自适应鲁棒控制(ARC)策略，称之为时滞ARC (TARC)。TARC  通过时滞估计对未知动态进行逼近，对逼近误差具有鲁棒性。TARC既不需要 完整的系统模型，也不需要任何预先定义的不确定性界的知识来计算开关增益，从而避免 了开关增益的高估和低估问题。[14]Roy基于  Lyapunov-Razumikhin定理进行了新的稳定性 分析，并提出了一种时滞估计方法(TDE)基于ARC框架。[15]为了减小无状态导数时测量误差 的影响，提出了一种新的基于TDE的控制器及其ARC框架，提出了基于  Lyapunov- Krasovskii的TDE设计稳定性概念，作为Lyapunov-Razumikhin  设计的替代/并行研究。与 基于TDE的控制律相比，提出了一种新的无需系统动力学知识的ARC控制策略。Roy解决了时 滞控制(TDC)中长期存在的连续时间一致稳定性分析与控制设计问题。基于新提出的TDE误 4 CN 111580387 A 说　明　书 2/12 页 差结构，提出了一种更为鲁棒的控制律。[16]Roy做出了许多重要贡献：提出了一种不需要先 验有界不确定性的自适应滑模控制(ASMC)方法；[17]提出了一种新的ASMC控制策略，克服了 传统ASMC中存在的欠估计和过估计问题；[18]提出了一种用于非完整轮式移动机器人精确 路径跟踪的时滞滑模混合控制方法[19]。 但是，经发明人调研，上述ASMC、TDE、ARC等控制方法在控制时间上反应较慢，并且 需要调控过多的控制输入，在控制效率上还未能达到较好的效果，进而对船舶运动时的平 衡控制造成影响，故此，本领域亟待一种解决前述问题的控制方法。 [1]Sorensen  A  J .A  survey  of  dynamic  positioning  control  systems[J] .Annual  Reviews  in  Control,2011,35(1):123-136. [2]Nguyen  T  D,Sorensen  A  J ,Quek  S  T.Design  of  hybrid  controller  for  dynamic  position  from  calm  to  extreme  sea  conditions[J] .Automatica ,2007 ,43 (5):768-785. [3]Nguyen  T  D .Design  of  hybrid  marine  control  system  for  dynamic  positioning[D].Singapore:National  University,2011. [4]Lindegaard  K  P .Acceleration  feedback  in  dynamic  positioning[D] .Trondheim:Norwegian  University  of  Science  and  Technology,2003. [5]XU  Haixiang .FengHui.Principle  of  ship  dynamic  positioning  system [M]，Beijing：National  Defense  Industry  Press，2016. [6]Jinqiang  Wang ,Cong  Wang ,Yingjie  Wei ,ChengjuZhang .  Sliding  mode  based  neural  adaptive  formation  control  of  underactuated  AUVs  with  leader- follower  strategy.Applied  Ocean  Research,2020,94:1-9. [7]Jianjun  Zhang ,Weidong  Liu ,Li 'eGao ,Le  Li ,Zeyu  Li .The  master  adaptive  impedance  control  and  slave  adaptive  neural  network  control  in  underwater  manipulator  uncertainty  teleoperation.Ocean  Engineering  165(2018) 465–479. [8]SHAO  Jingfeng .Research  on  ship  dynamic  positioning  control  based  on  sliding  mode  variable  structure[D].Dalian:Dalian  Maritime  University,2015. [9]DAI  Changsheng.Research  on  Adaptive  Iterative  sliding  Mode  Control  for  Underactuated  ship  Motion[D].Dalian:Dalian  Maritime  University,2017. [10]QIN  Chaoyu .Active  Disturbance  Rejection  Control  for  Ship  Path  Following  Based  Terminal  Sliding  Mode[D].Dalian:Dalian  Maritime  University, 2017. [11]WANG  Yuqi .Terminal  Sliding  Mode  Control  for  Tracking  and  Formation  of  Underactuated  Surface  Vessels[D] .Dalian:Dalian  Maritime  University,2017. [12]Yaoyao  Wang ,Kangwu  Zhu,Fei  Yan,Bai  Chen.Adaptive  super-twisting  nonsingular  fast  terminal  sliding  mode  control  for  cable-driven  manipulators  using  time-delay  estimation[J].Advances  in  Engineering  Software,2019,128:113- 124. 5 CN 111580387 A 说　明　书 3/12 页 [13]Yue  Zhao,Jiahui  Wang,Fei  Yan,Yi  Shen.Adaptive  sliding  mode  fault- tolerant  control  for  type-2  fuzzy  systems  with  distributed  delays[J] .Information  Sciences,2019,473:227-238. [14]Spandan  Roy ,Indra  Narayan  Kar ,Jinoh  Lee ,Nikos  G .  Tsagarakis , Darwin  G .Caldwell .Adaptive-robust  control  of  a  class  of  EL  systems  with  parametric  variations  using  artificially  delayed  input  and  position  feedback [J].IEEE  Transactions  on  Control  Systems  Technology,2019,27(2) ,603–615. [15]Spandan  Roy ,Indra  Narayan  Kar .Adaptive-Robust  Control  with  Limited  Knowledge  on  Systems  Dynamics:An  Artificial  Input  Delay  Approach  and  Beyond[M].Springer  Nature  Singapore  Pte  Ltd.  2020. [16]Spandan  Roy ,Jinoh  Lee ,Simone  Baldi .A  new  continuous-time  stability  perspective  of  time-delay  control:Introducing  a  state-dependent  upper  bound  structure.IEEE  Control  Systems  Letters[J],2019,3(2):475–480. [17]Spandan  Roy ,Simone  Baldi ,Leonid  M .Fridman .On  adaptive  sliding  mode  control  without  a  priori  bounded  uncertainty[J] .  Automatica ,Volume  111January  2020Article  108650. [18]Spandan  Roy,SayanBasu  Roy,Jinoh  Lee,Simone  Baldi.  Overcoming  the  underestimation  and  overestimation  problems  in  adaptive  sliding  mode  control [J].IEEE/ASME  TRANSACTIONS  ON  MECHATRONICS,2019,24(5):2031-2039. [19]Spandan  Roy,SubhajitNandy,Ranjit  Ray,SankarNathShome.  Time  delay  sliding  mode  control  of  nonholonomic  wheeled  mobile  robot:  experimental  validation[C].2014IEEE  International  conference  on  robotics&automation(ICRA) , Hong  Kong,China:2886-2892.
技术实现要素：
本发明的主要目的在于提供一种基于时滞分数阶船舶运动自适应滑模控制方法， 当船舶受海浪或运动量影响时，能快速恢复其稳定状态，以实现自主平衡。 为了实现上述目的，本发明提供了如下技术： 一种基于时滞分数阶船舶运动自适应滑模控制方法，所述控制方法包括以下步 骤： S1，建立目标虚拟船舶运动模型，以此设立数学模型； S2，求取步骤S1中数学模型中的状态空间； S3，根据系统的期望状态，求取状态误差； S4，将步骤S3中的状态误差代入，构造滑动模态曲面函数； S5，利用控制输入和最近时刻的状态信息来逼近系统的不确定性，构造自适应控 制律，以对滑模进行控制。 优选地，所述步骤S1中，数学模型的设立将选取纵荡、横荡和艏摇三自由度运动作 为参考值，建立二维坐标轴，其数学模型为： 6 CN 111580387 A 说　明　书 4/12 页 其中，x为前进位置，y为横荡位置，η＝[x  y ψ]T为姿向量，R为旋转矩阵。 优选地，所述步骤S1还包括设立船舶高速和低速运动的动力学模型，其模型为： 其中，u为前进速度，v为横荡速度，r为艏摇角速度，υ＝[u  v  r]T为速度向量，M为 惯性矩阵，D为阻尼矩阵，R为旋转矩阵，τ1为合成力矩，τω为外部干扰环境。 优选地，所述步骤S2中求取状态空间过程包括定义ξ(t)为非线性系统函数，τ(t) 为输入： τ(t)＝RM-1τ1(t)； 以及取状态变量：x(t)＝η(t)； 得出状态空间： 优选地，所述步骤S3中的状态误差为： 其中，xd为期望状态，为误差状态。 优选地，所述步骤S4中滑动模态曲面函数为： 其中，0＜α＜1,c>0。 优选地，所述步骤S5中包括当存在延时h时，TDC利用控制输入和最近时刻的状态 信息来逼近系统的不确定性，此时的状态空间为： 其中，TDC为时滞控制，ξ(t-h)为非线性系统函数，τ(t-h)为输入。 优选地，所述步骤S5中的自适应控制率构造如下： 优选地，所述步骤S5中自适应控制律的增益如下： 其中， 另外，与所述控制方法相对应的，本发明还提供一种基于时滞分数阶自适应的滑 模控制系统，其包括： 模型创建模块，用于建立目标虚拟船舶运动模型，以此设立数学模型； 7 CN 111580387 A 说　明　书 5/12 页 状态计算模块，用于求取所述数学模型中的状态空间；并根据系统的期望状态，求 取状态误差； 函数构造模块，用于将所述状态误差代入，构造滑动模态曲面函数； 滑模控制模块，其利用控制输入和最近时刻的状态信息来逼近系统的不确定性， 构造自适应控制律，以对滑模进行控制。 本发明实施例具有以下有益效果：本发明实施例证明了闭环系统的稳定性，其实 验结果表明，通过使用本发明中的自适应滑模控制算法能使船舶在受到干扰时自动调整， 快速恢复其稳定状态，提升了船舶中对滑模的控制效率，提高了船舶制动控制的精度及稳 定性。 附图说明 构成本发明的一部分的附图用来提供对本发明的进一步理解，使得本发明的其它 特征、目的和优点变得更明显。本发明的示意性实施例附图及其说明用于解释本发明，并不 构成对本发明的不当限定。在附图中： 图1是本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的流程示意 图； 图2是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的坐标 轴示意图； 图3是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的参数 表； 图4是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图5是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图6是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图7是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图8是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图9是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响应 曲线变化图； 图10是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图11是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图12是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图13是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 8 CN 111580387 A 说　明　书 6/12 页 应曲线变化图； 图14是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图15是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图16是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图17是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图； 图18是本发明本发明种基于时滞分数阶自适应的滑模控制方法中一个可选的响 应曲线变化图；