技术摘要：
本发明提供了一种保证凸轮机构运动可靠性的优化设计方法，包括如下步骤：步骤1，通过分析基本尺寸误差、运动副间隙误差对盘形凸轮机构运动精度的影响，建立考虑两种误差的摆动推杆盘形凸轮机构运动可靠性R、可靠性灵敏度Sσ(i)数学模型。步骤2，依据盘形凸轮机构优化模  全部
背景技术：
随着结构、机构可靠性分析方法和设计理论及其它相关安全理论日渐成熟，盘形 凸轮机构构件发生强度故障而引起的事故已越来越少。相比之下，盘形凸轮机构的运动精 度问题则显得日益突出。由于构件存在尺寸、间隙、磨损等误差，从而使各构件的运动误差 具有不确定性，导致运动精度下降。所以为保证盘形凸轮机构的运动精度，对其进行误差分 析及可靠性定量计算显得尤为重要。 智能优化算法是受人类智能、生物群体社会性或自然现象规律的启发，利用计算 机模拟特殊行为而用于求解组合优化问题的有效途径。盘形凸轮机构最优参数尺寸组合的 寻找过程也可定义为一种求解最优参数组合的多目标优化问题。正弦余弦算法因参数少易 实现、逻辑简明清晰且运算速度快而在实际工程问题中得到广泛应用。但标准正弦余弦算 法仍存在易早熟、迭代后期难以跳出局部最优等问题。
技术实现要素：
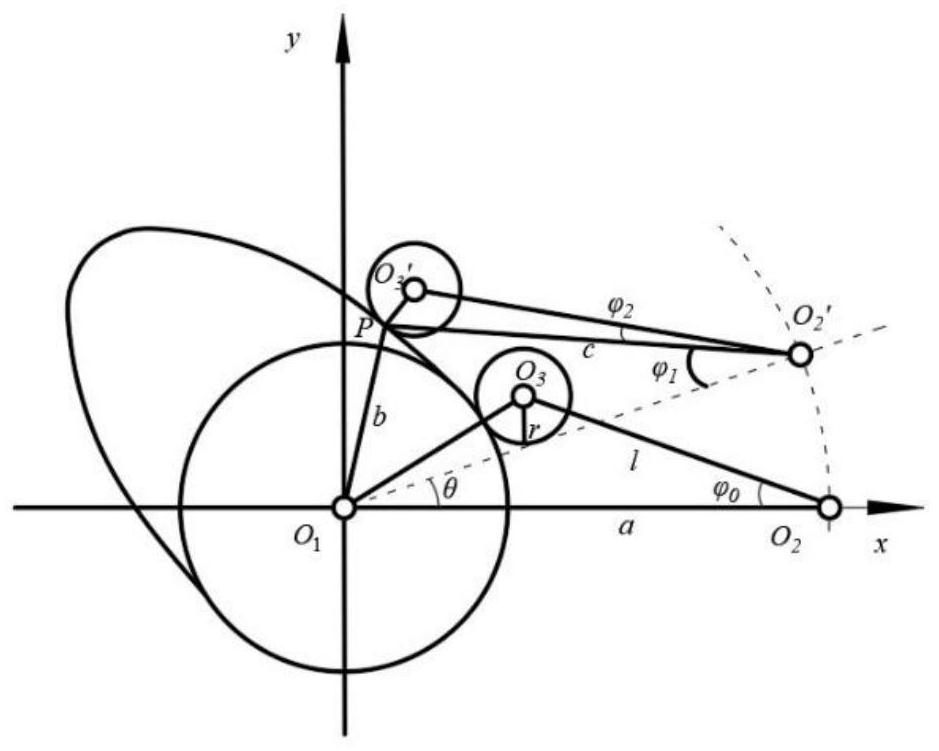
发明目的：为了使盘形凸轮机构在考虑基本尺寸误差、运动副间隙误差条件下的 运动可靠性最大化，且改善现有标准正弦余弦算法易早熟、迭代后期易陷入局部最优等问 题，提出一种嵌入边界缓冲策略的正弦余弦算法。改进后的算法较好的解决了个体越界行 为，提高了种群多样性，增强了算法寻优精度，从而达到更好的优化盘形凸轮机构最优参数 尺寸组合的目的。 技术方案：为实现上述目的，本发明提供一种保证凸轮机构运动可靠性的优化设 计方法，包括如下步骤： (1)通过分析基本尺寸误差、运动副间隙误差对盘形凸轮机构运动精度的影响，建 立考虑两种误差的摆动推杆盘形凸轮机构运动可靠性R、可靠性灵敏度Sσ(i)数学模型。 (2)依据盘形凸轮机构优化模型的要求，确定盘形凸轮机构中摆杆长l、滚子半径 r、凸轮轴轴心与摆动回转中心距离a、铰链运动副间隙zg、凸轮及滚子接触点与凸轮轴轴心 距b等各项参数优化范围、允许尺寸误差及分布类型等指标，并建立盘形凸轮机构轮廓曲线 方程。 (3)利用改进正弦余弦算法在解空间内对各参数组合进行优化，并以盘形凸轮机 构运动一周内的最小可靠度值作为评判标准，得到最优参数组合。 (4)依据步骤3所得结论对该类盘形凸轮机构模型提出合理的改进意见。 步骤(1)中考虑基本尺寸误差、运动副间隙误差，构建对应计算模型： 1)摆动推杆盘形凸轮机构示意图如附图1所示，令初始位置时摆杆与x轴间夹角为 则任意位置摆杆摆角表达式为： 5 CN 111611727 A 说　明　书 2/8 页 2)运用泰勒级数展开法对各变量二阶展开，可得由基本尺寸误差所引起的摆杆摆 角位置误差 3)因基本参数x、y、r、l、a均为随机变量且符合正态分布，故可求得由基本尺寸误 差所引起的摆杆摆角位置误差均值与方差： 4)运动副非连续接触模型如附图2、3所示，设凸轮与支座连接处销轴中心坐标为O (x1,y1)，滚子与摆杆连接处销轴中心坐标为O3(x2,y2)，将各尺寸参数a、b、l、r分别利用有效 长度理论进行替换： 5)按泰勒级数展开法进行二阶展开，可得由运动间隙所引起的摆杆摆角位置误差 6)因x1、x2、y1、y2皆为随机变量且服从正态分布,故可知由运动副间隙所引起的摆 杆摆角位置误差均值与方差： 根据步骤(2)，结合附图1，对盘形凸轮机构轮廓曲线方程进行定义： 1)轮廓曲线: 2)推程曲线: P＝acosθ-lcosα(1 0.3491sinθ) Q＝-asinθ lsinα(1 0.3491sinθ) α＝θ-0.3491cosθ 0.667 3)回程曲线: 6 CN 111611727 A 说　明　书 3/8 页 P＝acosθ-lcosα(1-0.3491sin(θ-π)) Q＝-asinθ lsinα(1-0.3491sin(θ-π)) α＝θ 0.3491cos(θ-π) 0.667 步骤(1)中考虑存在基本尺寸误差、运动副间隙误差，定义盘形凸轮机构运动可靠 性R： 其中Φ(·)为标准正态分布函数，δ为给定机构允许总误差，服从正态分布； 分别为基于上述两种误差所得摆杆摆角位置误差均值、标准差。由此可知各参数 的标准差对机构运动可靠性的灵敏度Sσ(i)： 式中φ(·)为标准正态分布的概率密度函数，i∈(a、l、b、r、zg)。 步骤(3)中采用改进正弦余弦算法对盘形凸轮机构参数组合在解空间内进行优 化，其过程分为如下几步： 1)参数初始化，假设种群规模为m，种群中任意个体由d维分量构成，第t代时个体i 可表示为： 其中i∈{1,2,… ,m}，j∈{1,2,…,d}。首先 在解空间内随机初始化种群： ub、lb分别为解空间上下 限。 2)将全部个体每一维所对应的不同参数(a、l、b、r、zg)代入适应度函数中，得到相 应个体的适应度值。取种群内最优个体的位置为popbest，并设其为初始全局最优值。 3)依据初始化所得各项前置条件进行迭代更新： 其中，popbest随t的增加而不断更新；r2、r3、r4均为均匀分布的随机数，r2∈[0,2π]， 决定当前解是否靠近最优解；r3∈[0,2]，控制最优解对当前解的影响程度；r4∈[0,1]，主要 影响正弦、余弦机制切换，由上式可知当r1sin(r2)或r1cos(r2)大于1或小于-1时，进行全局 搜索；介于-1与1之间时，进行局部开发；r1＝2-2t/T，其定义个体下次迭代的最大可能移动 范围，起平衡算法全局搜索能力与局部开发能力的作用，T为最大迭代次数。 4)判断个体每一维参数是否存在超出解空间上下限的情况，若否，则转到步骤5)； 若是，则对个体该维参数进行边界缓冲处理： 式中ε为缓冲控制系数，取缓冲上下边界分别为popMax＝0.1*ub、popMin＝0.1* lb，当个体超越上边界时： 7 CN 111611727 A 说　明　书 4/8 页 当个体超越下边界时： 6)更新种群适应度最优值，并判断是否达到最大迭代次数条件，若否，则转到步骤 3)；若是，则输出最优参数组合及对应的运动可靠性曲线、运动可靠性灵敏度曲线。 本发明与以往技术相比，做了如下改进：(1)对标准正弦余弦算法进行改进，通过 嵌入边界缓冲策略解决了个体越界问题，丰富了种群的多样性，提高算法寻优精度。(2)本 发明综合考虑了基本尺寸误差与运动副间隙误差的影响，建立了摆动推杆盘形凸轮机构的 运动可靠性分析模型及可靠性灵敏度分析模型，并利用改进正弦余弦算法求解盘形凸轮机 构参数组合问题，相比传统穷举法而言极大的提高了运算速度，同时得出在该参数组合下 的运动可靠性曲线及运动可靠性灵敏度曲线，便于分析、研究盘形凸轮机构运动特性，所得 结论具有较大的工程参考价值。 下面结合说明书附图对本发明作进一步描述。发明目的：为了使盘形凸轮机构在 考虑基本尺寸误差、运动副间隙误差条件下的运动可靠性最大化，且改善现有标准正弦余 弦算法易早熟、迭代后期易陷入局部最优等问题，提出一种嵌入边界缓冲策略的正弦余弦 算法。改进后的算法较好的解决了个体越界行为，提高了种群多样性，增强了算法寻优精 度，从而达到更好的优化盘形凸轮机构最优参数尺寸组合的目的。 技术方案：为实现上述目的，本发明提供一种保证凸轮机构运动可靠性的优化设 计方法，包括如下步骤： (1)通过分析基本尺寸误差、运动副间隙误差对盘形凸轮机构运动精度的影响，建 立考虑两种误差的摆动推杆盘形凸轮机构运动可靠性R、可靠性灵敏度Sσ(i)数学模型。 (2)依据盘形凸轮机构优化模型的要求，确定盘形凸轮机构中摆杆长l、滚子半径 r、凸轮轴轴心与摆动回转中心距离a、铰链运动副间隙zg、凸轮及滚子接触点与凸轮轴轴心 距b等各项参数优化范围、允许尺寸误差及分布类型等指标，并建立盘形凸轮机构轮廓曲线 方程。 (3)利用改进正弦余弦算法在解空间内对各参数组合进行优化，并以盘形凸轮机 构运动一周内的最小可靠度值作为评判标准，得到最优参数组合。 (4)依据步骤3所得结论对该类盘形凸轮机构模型提出合理的改进意见。 步骤(1)中考虑基本尺寸误差、运动副间隙误差，构建对应计算模型： 2)摆动推杆盘形凸轮机构示意图如附图1所示，令初始位置时摆杆与x轴间夹角为 则任意位置摆杆摆角表达式为： 3)运用泰勒级数展开法对各变量二阶展开，可得由基本尺寸误差所引起的摆杆摆 角位置误差 8 CN 111611727 A 说　明　书 5/8 页 4)因基本参数x、y、r、l、a均为随机变量且符合正态分布，故可求得由基本尺寸误 差所引起的摆杆摆角位置误差均值与方差： 5)运动副非连续接触模型如附图2、3所示，设凸轮与支座连接处销轴中心坐标为O (x1,y1)，滚子与摆杆连接处销轴中心坐标为O3(x2,y2)，将各尺寸参数a、b、l、r分别利用有效 长度理论进行替换： 6)按泰勒级数展开法进行二阶展开，可得由运动间隙所引起的摆杆摆角位置误差 7)因x1、x2、y1、y2皆为随机变量且服从正态分布,故可知由运动副间隙所引起的摆 杆摆角位置误差均值与方差： 根据步骤(2)，结合附图1，对盘形凸轮机构轮廓曲线方程进行定义： 2)轮廓曲线: 3)推程曲线: P＝acosθ-lcosα(1 0.3491sinθ) Q＝-asinθ lsinα(1 0.3491sinθ) α＝θ-0.3491cosθ 0.667 3)回程曲线: P＝acosθ-lcosα(1-0.3491sin(θ-π)) Q＝-asinθ lsinα(1-0.3491sin(θ-π)) α＝θ 0.3491cos(θ-π) 0.667 步骤(1)中考虑存在基本尺寸误差、运动副间隙误差，定义盘形凸轮机构运动可靠 9 CN 111611727 A 说　明　书 6/8 页 性R： 其中Φ(·)为标准正态分布函数，δ为给定机构允许总误差，服从正态分布； 分别为基于上述两种误差所得摆杆摆角位置误差均值、标准差。由此可知各参数 的标准差对机构运动可靠性的灵敏度Sσ(i)： 式中φ(·)为标准正态分布的概率密度函数，i∈(a、l、b、r、zg)。 步骤(3)中采用改进正弦余弦算法对盘形凸轮机构参数组合在解空间内进行优 化，其过程分为如下几步： 1)参数初始化，假设种群规模为m，种群中任意个体由d维分量构成，第t代时个体i 可表示为： 其中i∈{1,2,… ,m}，j∈{1 ,2,… ,d}。首先 在解空间内随机初始化种群： ub、lb分别为解空间上下 限。 2)将全部个体每一维所对应的不同参数(a、l、b、r、zg)代入适应度函数中，得到相 应个体的适应度值。取种群内最优个体的位置为popbest，并设其为初始全局最优值。 3)依据初始化所得各项前置条件进行迭代更新： 其中，popbest随t的增加而不断更新；r2、r3、r4均为均匀分布的随机数，r2∈[0,2π]， 决定当前解是否靠近最优解；r3∈[0,2]，控制最优解对当前解的影响程度；r4∈[0,1]，主要 影响正弦、余弦机制切换，由上式可知当r1sin(r2)或r1cos(r2)大于1或小于-1时，进行全局 搜索；介于-1与1之间时，进行局部开发；r1＝2-2t/T，其定义个体下次迭代的最大可能移动 范围，起平衡算法全局搜索能力与局部开发能力的作用，T为最大迭代次数。 4)判断个体每一维参数是否存在超出解空间上下限的情况，若否，则转到步骤5)； 若是，则对个体该维参数进行边界缓冲处理： 式中ε为缓冲控制系数，取缓冲上下边界分别为popMax＝0.1*ub、popMin＝0.1* lb，当个体超越上边界时： 当个体超越下边界时： 10 CN 111611727 A 说　明　书 7/8 页 7)更新种群适应度最优值，并判断是否达到最大迭代次数条件，若否，则转到步骤 3)；若是，则输出最优参数组合及对应的运动可靠性曲线、运动可靠性灵敏度曲线。 本发明与以往技术相比，做了如下改进：(1)对标准正弦余弦算法进行改进，通过 嵌入边界缓冲策略解决了个体越界问题，丰富了种群的多样性，提高算法寻优精度。(2)本 发明综合考虑了基本尺寸误差与运动副间隙误差的影响，建立了摆动推杆盘形凸轮机构的 运动可靠性分析模型及可靠性灵敏度分析模型，并利用改进正弦余弦算法求解盘形凸轮机 构参数组合问题，相比传统穷举法而言极大的提高了运算速度，同时得出在该参数组合下 的运动可靠性曲线及运动可靠性灵敏度曲线，便于分析、研究盘形凸轮机构运动特性，所得 结论具有较大的工程参考价值。 下面结合说明书附图对本发明作进一步描述。 附图说明 下面结合附图和