技术摘要：
本发明公开了一种面向天基光学监视的GEO目标自主弧段关联与定轨方法，涉及航天技术领域，具备高关联正确率和定轨精度。本发明首先利用任意两个短弧初轨对应的位置矢量进行Lambert方程求解，得到较高精度的初轨半长轴，并利用近圆轨道假设对测角数据点进行距离赋值，进  全部
背景技术：
实现全球空间目标的常态化监视是利用太空的基础，美国、俄罗斯、法国、日本等 世界大国相继组建太空目标监视“国家队”，承担对太空目标的探测编目和侦察监视任务。 GEO卫星在全球通信、侦察、预警等领域具有广泛用途，属于稀缺的太空战略资源。对全球 GEO目标进行完备的探测编目，确定目标轨位和行为意图具有重要意义。 天基光学监视卫星具有全球巡视的特点，能够快速搜索扫描或者凝视跟踪多个 GEO目标，若采用太阳同步轨道或者小倾角轨道，还可有效抑制天光和地气光影响，提升探 测能力。在获取到GEO目标观测数据后，天基光学监视最为关键的环节就是对数据进行弧段 间关联定轨，完成自主编目维持。空间目标自主编目的一般流程是在短弧定轨的基础上，对 于无历史轨道根数的目标，进行两两短弧间的关联定轨，形成新的目标轨道根数；对于有历 史轨道根数的目标，利用短弧数据对历史根数进行轨道改进和编目维持。建立一套具有较 高关联成功率和定轨精度的GEO目标天基观测数据的自主编目方法，是支撑新目标发现、异 动检测和抵近告警等技术应用的基础。 然而，天基光学观测数据的自主关联与定轨存在一些系统性的难点问题。由于卫 星平台自身运行速度快，导致对每个GEO目标的观测弧段短，短弧初轨确定的收敛性和精度 都得不到保证。同时，天基平台在惯性系下的轨道面指向相对固定，若不采用大幅姿态机 动，获取的观测弧段在惯性系下的位置较为固定，几何分布稀疏，实现自主的关联和高精度 的定轨编目十分困难。 针对天基光学监视的GEO目标自主弧段关联与定轨需求，寻找一种关联正确率和 精度高的弧段间关联和定轨方法，对于提升天基光学监视卫星对GEO目标的自主编目效能 十分必要。
技术实现要素：
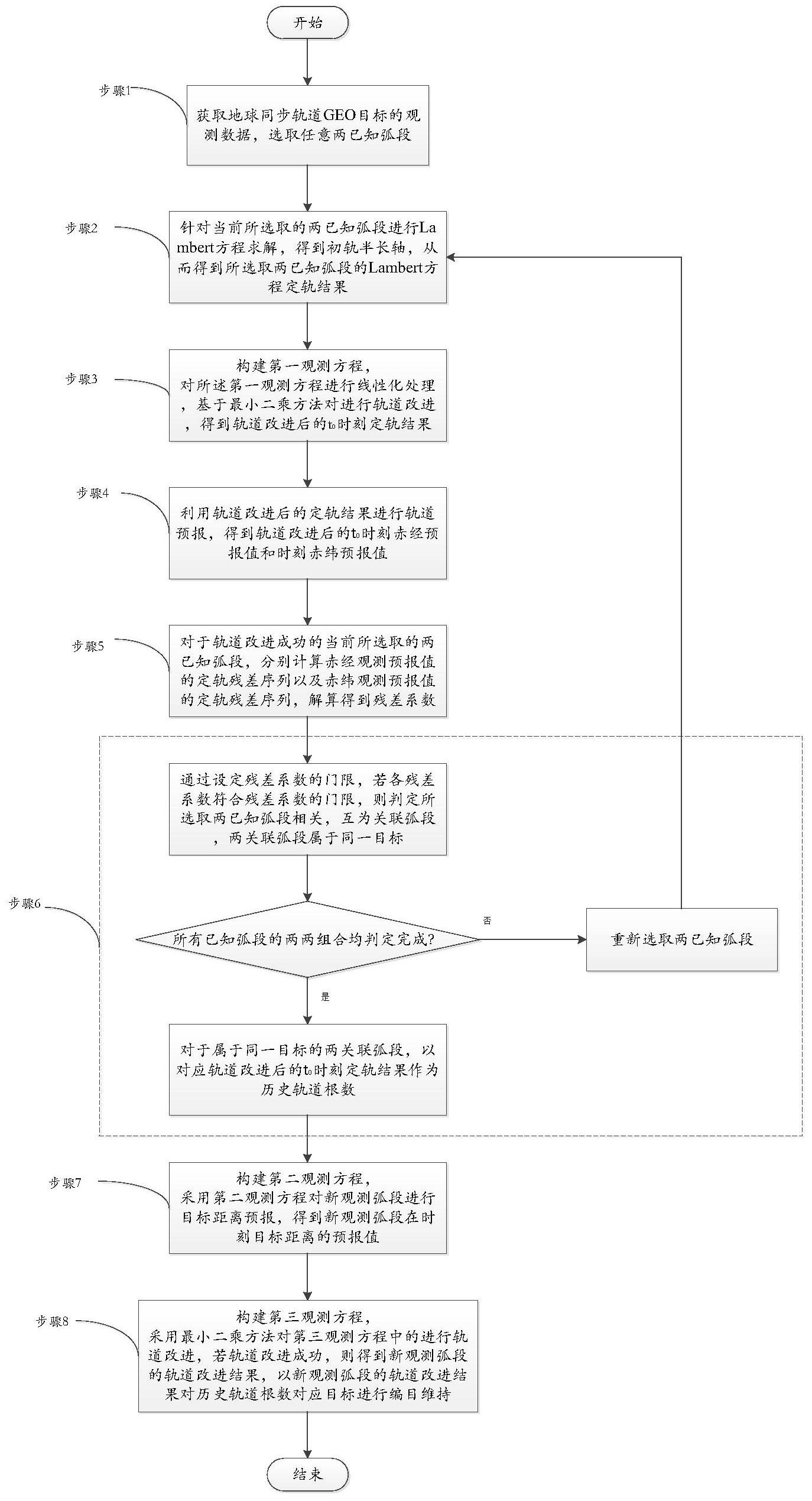
有鉴于此，本发明提供了一种面向天基光学监视的GEO目标自主弧段关联与定轨 方法，能够解决仅光学测角数据的天基观测短弧段间自主关联和高精度定轨的难题。 为达到上述目的，本发明的技术方案为：一种面向天基光学监视的GEO目标自主弧 段关联与定轨方法，包括如下步骤： 步骤1、获取地球同步轨道GEO目标的观测数据，选取任意两已知弧段。 步骤2、针对当前所选取的两已知弧段进行Lambert方程求解，得到初轨半长轴，从 而得到所选取两已知弧段的Lambert方程定轨结果，即为历元初始时刻t0时刻的初轨根数 σLambert(t0)；t0为历元初始时刻； 步骤3、构建第一观测方程：[ρi(ti) ,αi(ti) ,δi(ti)]＝H(σLambert(t0) ,ti-t0) V； 5 CN 111578950 A 说　明　书 2/7 页 其中ti为历元第i个时刻，ρi(ti)为ti时刻观测目标的距离假设值、αi(ti)为ti时刻 赤经观测值，δi(ti)为ti时刻赤纬观测值，H(σLambert(t0) ,ti-t0)为以σLambert(t0)为初始值代 入的轨道预报的理论观测函数，V为测量误差； 对第一观测方程进行线性化处理，基于最小二乘方法对进行轨道改进，得到轨道 改进后的t0时刻定轨结果σχ(t0)； 步骤4、利用轨道改进后的定轨结果σχ(t0)进行轨道预报，得到轨道改进后的ti时 刻赤经预报值 和ti时刻赤纬预报值 步骤5、对于轨道改进成功的当前所选取的两已知弧段，分别计算赤经观测预报值 的定轨残差序列以及赤纬观测预报值的定轨残差序列，解算得到残差系数，包括赤经观测 预报值的定轨残差序列的一阶趋势量系数以及赤纬观测预报值的定轨残差序列的一阶趋 势量系数； 步骤6、通过设定残差系数的门限，若各残差系数符合残差系数的门限，则判定所 选取两已知弧段相关，互为关联弧段，两关联弧段属于同一目标； 重新选取两已知弧段，返回步骤2，直至所有已知弧段的两两组合均判定完成； 对于属于同一目标的两关联弧段，以对应轨道改进后的t0时刻定轨结果σχ(t0)作 为历史轨道根数，执行步骤7； 步骤7、构建第二观测方程： H(σχ(t0) ,ti-t0)为以历史轨道根数σχ(t0)代入的轨道预报的理论观测函数；依据 ti时刻赤经观测预报值 ti时刻赤纬观测预报值 采用第二观测方程对新观测弧 段进行目标距离预报，得到新观测弧段在ti时刻目标距离的预报值 步骤8、构建第三观测方程： H(σχ(t0) ,ti-t0)为以历史轨道根数σχ(t0)代入的轨道预报的理论观测函数。 依据新观测弧段的ti时刻赤经观测值αi(ti)及新观测弧段ti时刻赤纬观测值δi (ti)，ti时刻目标距离的预报值 采用最小二乘方法对第三观测方程中的σχ(t0)进行 轨道改进，若轨道改进成功，则得到新观测弧段的轨道改进结果，以新观测弧段的轨道改进 结果对历史轨道根数σχ(t0)对应目标进行编目维持。 进一步地，步骤2中，针对当前所选取的两已知弧段进行Lambert方程求解，得到初 轨半长轴，从而得到所选取两已知弧段的Lambert方程定轨结果，即为历元初始时刻t0时刻 的初轨根数σLambert(t0)；具体为： 对于当前所选取的两已知弧段，其中第一弧段的定轨结果为历元t1时刻的轨道根 数σinitial(t1)，t1为第一弧段对应的历元时刻，其取值为第一弧段对应的观测时段，根据二 体问题解算得到第一弧段t1时刻的位置矢量为 第二个弧段的定轨结果为历元t2时刻的 轨道根数σinitial(t2)，t2为第二弧段对应的历元时刻，其取值为第二弧段对应的观测时段， 计算第二弧段t2时刻的位置矢量为 建立Lambert方程： t2-t1＝(a3/μ)1/2[(ψ-sinψ)-(ε-sinε)]； 6 CN 111578950 A 说　明　书 3/7 页 其中a为轨道半长轴，μ为地球引力常数，ψ是关于第一弧段t1时刻的位置矢量 的 函数、ε是关于第二弧段t2时刻的位置矢量 的函数： 的二范数为 的二范数为 第一弧段和第二弧段之间的矢量 二范数为 ||·||2表示矢量的二范数。 通过对Lambert方程迭代求解轨道半长轴a，从而所选取两已知弧段的Lambert方 程定轨结果，即为历元初始时刻t0时刻的初轨根数σLambert(t0)；t0为历元初始时刻。 进一步地，步骤5中，具体为：所选取的两已知弧段为A和B； 利用轨道改进后的定轨结果σχ(t0)进行轨道预报，得到轨道改进后的ti时刻赤经 预报值 和ti时刻赤纬预报值 在当前所选取的一个已知弧段对应的时段Slot内，分别取其中S个观测时刻的赤 经观测预报值 和赤纬观测预报值 由此得到S个观测时刻的赤经观测预报值的定轨残差序列{Δαs,s＝1,2,...,S}， 以及赤纬观测预报值的定轨残差序列{Δδs ,s＝1 ,2 ,...,S}， s为时段Slot内第s个观测时刻；αs为时段Slot内第s个观测时刻赤经观测值， δs为时段Slot内第s个观测时刻赤纬观测值。 构建方程组： 其中a0为赤经系统偏差系数，a1为赤经定轨误差一阶趋势量系数，b0为赤纬系统偏 差系数，b1为赤纬定轨误差一阶趋势量。 通过最小二乘估计求解弧段A和B对应的残差系数a0、a1、b0和b1。 其中弧段A对应的赤经定轨误差一阶趋势量系数记为 赤纬定轨误差一阶趋势 量 弧段B对应的赤经定轨误差一阶趋势量系数记为 赤纬定轨误差一阶趋势量 步骤6，通过设定残差系数的门限，若各残差系数符合残差系数的门限，则判定所 选取两已知弧段相关，互为关联弧段，两关联弧段属于同一目标，具体为： 设定残差系数门限为5角秒/分钟；若满足： 则判定弧段A和B相关，互为关联弧段，两关联弧段属于同一目标。 进一步地，若当前已知弧段与一个以上其他已知弧段相关，则从一个以上其他已 知弧段中优选一阶趋势量系数最小者作为当前已知弧段的关联弧段。 7 CN 111578950 A 说　明　书 4/7 页 进一步地，步骤8中，若新观测弧段的针对一个以上的历史轨道根数进行的轨道改 进均成功，则从一个以上的历史轨道根数对应目标中，优选对应关联弧段一阶趋势量系数 最小者进行编目维持。 有益效果： 本发明提出了一种天基光学监视的GEO目标自主弧段关联与定轨方法。该方法的 核心是对于任意两两短弧进行Lambert方程求解，提升初轨半长轴精度，并对测角数据点进 行距离初值假设，完成摄动条件下的初轨改进，比对初轨改进结果与原始观测角度的差异， 选择观测残差斜率作为判决门限进行弧段间关联。以两弧段间关联的初轨结果作为编目库 起始根数，进行新观测弧段的自主距离预报，结合测角数据，实现稳健的编目轨道更新和维 持，解决了传统技术中仅光学测角数据的天基观测短弧段间自主关联和高精度定轨的难 题。 附图说明 图1为本发明实施例提供的一种面向天基光学监视的GEO目标自主弧段关联与定 轨方法流程图； 图2为天基光学监视的多弧段关联正确率与定轨精度变化情况。