技术摘要:
本发明公开了一种基于均匀化理论的页岩基质流固耦合尺度升级方法,建立了一种页岩基质流固耦合尺度升级方法,能够将微尺度上有机质和无机质各自特征有效地表征到宏观模拟中。首先,将页岩基质看成是由有机质和无机质组成的非均质多孔弹性介质,考虑真实气体在这两种介 全部
背景技术:
页岩气资源分布广、储量大,但其基质渗透率极低,通常需要经过水力压裂才能进 行商业化开采,压裂后的页岩储层具有多尺度孔缝特征,且处于复杂地应力场和渗流场的 共同作用中,流固耦合效应明显。其中,页岩基质作为气体的主要储集空间,其流固耦合模 型的建立是页岩气藏宏观流固耦合数值模拟的基础。由于页岩基质通常由微尺度的有机质 和无机质组成,而这两种介质的力学性质差异较大,且气体在两者中的赋存方式和流动机 制均不相同,要准确刻画气体在页岩基质中的流固耦合过程,需针对两种介质建立不同的 微尺度模型,但由于计算效率问题,微尺度模型无法直接用于宏观模拟。近年来,国内外学 者分别采用流量等效法和均匀化理论,对页岩基质中有机质分布对气体宏观渗流规律的影 响进行了研究,但均并未考虑流固耦合作用。因此,有必要建立一种尺度升级方法,将微尺 度上有机质和无机质各自特征有效地表征到页岩气藏宏观流固耦合模拟中,来解决上述问 题。
技术实现要素:
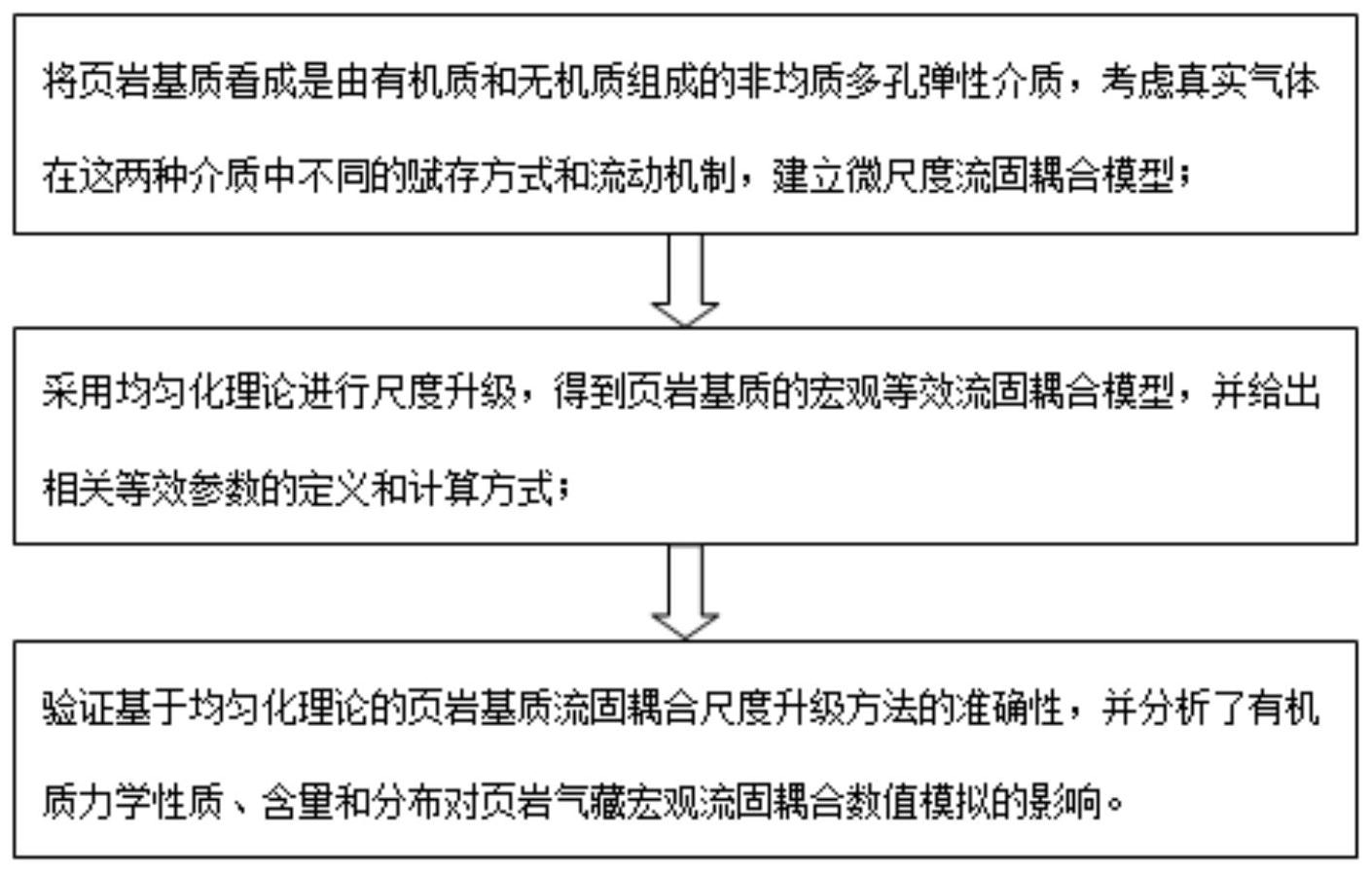
本发明的目的是提供一种基于均匀化理论的页岩基质流固耦合尺度升级方法,将 基于均匀化理论,建立考虑微尺度上有机质和无机质各自特征的页岩基质流固耦合尺度升 级方法,通过数值算例验证尺度升级方法的正确性,并分析有机质力学性质、含量和分布对 页岩气藏宏观流固耦合数值模拟的影响,来解决上述现有技术存在的问题。 为实现上述目的,本发明提供了如下方案:本发明提供了一种基于均匀化理论的 页岩基质流固耦合尺度升级方法,包括如下步骤: 将页岩基质看成是由有机质和无机质组成的非均质多孔弹性介质,考虑真实气体 在这两种介质中不同的赋存方式和流动机制,建立微尺度流固耦合模型; 采用均匀化理论进行尺度升级,得到页岩基质的宏观等效流固耦合模型,并给出 相关等效参数的定义和计算方式; 验证基于均匀化理论的页岩基质流固耦合尺度升级方法的准确性,并分析了有机 质力学性质、含量和分布对页岩气藏宏观流固耦合数值模拟的影响。 优选地,构建微尺度流固耦合模型的过程如下: 6 CN 111597721 A 说 明 书 2/12 页 式中,σ和σs分别表示总应力张量和有效应力张量;p为孔隙压力;α为Biot系数;I 为单位张量;C为弹性张量;us为骨架位移;β表示综合压缩系数;t表示时间;δ为克罗内克符 号;φ为孔隙度;mg表示吸附/解吸项;ρg为气体密度;v为气体流速;ka为气体的视渗透率;μ 为气体粘度; 根据小变形假设,应变张量e(us)定义如下: 综合压缩系数β和真实气体密度ρg的表达式如下: 式中,Ks为基质骨架体积模量;Mg为气体摩尔质量;Z表示气体压缩因子;R为通用气 体常数;T表示储层温度; 根据Langmuir等温吸附,气体吸附/解吸项mg的表达式如下: 式中,ρr表示岩石密度;ρgstd表示标准条件下的气体密度;VL和PL分别表示有机质 的Langmuir体积和Langmuir压力。 无机质中气体的运移机制主要为粘性流和Knudsen扩散,其视渗透率kai为: 有机质中气体的运移机制主要为粘性流、Knudsen扩散和表面扩散,其视渗透率kak 为: 式中, 为本征渗透率,其中rh和τ分别为孔隙半径和迂曲度;Kn=λ/reff 为Knudsen数,其中,λ为气体分子的平均自由程,reff为孔隙有效半径;b=-1为滑移系数;Ds 表示吸附气的表面扩散系数;Cmax和θ分别为有机质的最大吸附量和气体覆盖率: 所述页岩基质流固耦合模型的非均质系数在无机质和有机质中分别取值如下: 式中,下标i和k分别表示无机质和有机质;dm为甲烷分子直径。 优选地,采用均匀化理论进行尺度升级,得到页岩基质的宏观等效流固耦合模型, 并给出相关等效参数的定义和计算方式的具体过程如下: 考虑一个特征长度为L的页岩基质,由大量的周期性微尺度元胞组成,微尺度元胞 7 CN 111597721 A 说 明 书 3/12 页 的特征长度为l,引入不同特征长度之间的比值ε=l/L,所述页岩基质流固耦合模型中的变 量σ,us,v and p由以下渐进展开式近似: 式中,y=x/ε,y表示微观尺度坐标;x表示宏观尺度坐标; 表示关于坐标x、y以 及时间t的周期性变量; 根据链式准则,得到: 把方程(11)代入方程(1)~(3)中,并采用公式(12)进行变换,比较方程中不同阶 数ε的系数; 通过比较方程(3)中ε-1的系数以及方程(1)中ε-2的系数得到: 由此可知p(0)和us(0)仅在宏观尺度x上变化,与微观尺度y无关,即: p(0)=p(0)(x,t) ,us(0)=us(0)(x,t) (14) 通过比较方程(2)中ε-1的系数以及方程(3)中ε0的系数得到: 分别对v(0)和p(1)进行分离变量分析: 式中,ω和π均是关于y的周期性变量; 把式(16)代入式(15),得到元胞辅助方程: 式中,ei为笛卡尔坐标系中的i-方向的单位矢量; 对方程(16)中的v(0)在元胞上进行体积平均,得到宏观渗流方程: 式中,|Ω|为整个元胞的体积;表示变量a的体积平均,kequ为等效视渗透率张 量: 8 CN 111597721 A 说 明 书 4/12 页 比较方程(1)中ε-1的系数得到: 由此可知,us(1)为: 式中, 表示与坐标y无关的任意变量;与坐标y相关的周期性变量ξpq满足方 程: 式中,δ为克罗内克符号; 比较方程(1)中ε0的系数得到: 将方程(24)在元胞上进行体积平均,并采用散度定理和周期性边界条件,得到: 根据体积平均定理和周期性边界条件,整理得到宏观应力平衡方程: 式中,等效弹性张量Cequ和等效Biot系数αequ分别定义如下: Cequijkl=












