技术摘要：
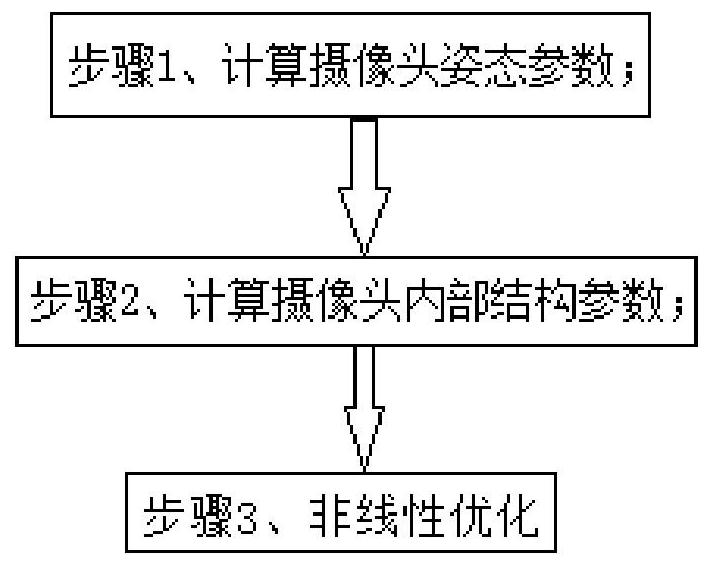
本发明提出一种快速高精度摄像头参数计算方法，所述方法包括如下步骤：步骤1、计算摄像头姿态参数；步骤2、计算摄像头内部结构参数；步骤3、在步骤1和步骤2已经求解出所需的摄像头参数后，将所求解出的参数作为初始化参数结合成像模型对参数做进一步的非线性优化。本发  全部
背景技术：
摄像头作为计算机视觉中的重要传感器被广泛应用于目标检测、目标识别等领 域。由于每个摄像头在出厂时无法保证各元器件结构的一致性，因此在使用之前需要进行 摄像头参数的计算，并根据计算出的参数和摄像头的成像模型来对摄像头进行标定。对于 一些畸变较小的摄像头通常采用小孔成像模型，成像模型比较简单且呈线性，但视场角较 小；对于一些大视场角需求的场景，通常采用广角摄像头，此时成像模型比较复杂且呈非线 性，在计算摄像头参数时计算过程复杂、耗时较长、计算精度较低。
技术实现要素：
本发明目的是为了解决现有技术中的问题，提出了一种快速高精度摄像头参数计 算方法。本发明所述方法计算简单并且精度高，通过将非线性求解转换成线性求解来降低 计算复杂度，并同时提高了结果的精度。 本发明是通过以下技术方案实现的，本发明提出一种快速高精度摄像头参数计算 方法，摄像头的成像模型如公式(1)所示： 其中，(u，v)是图像坐标，(X，Y)是真实世界物理坐标，(α0...αN)是摄像头内部结构 参数，(r，t)是摄像头在真实世界的姿态参数，r是摄像头在真实世界姿态的旋转参数，t  是 摄像头在真实世界姿态的平移参数； 所述方法包括如下步骤： 步骤1、计算摄像头姿态参数； 步骤2、计算摄像头内部结构参数； 步骤3、在步骤1和步骤2已经求解出所需的摄像头参数后，将所求解出的参数作为 初始化参数结合公式(1)对参数做进一步的非线性优化。 4 CN 111598954 A 说　明　书 2/5 页 进一步地，所述步骤1具体为： 根据公式(1)得到如下公式： vj.(r31Xj r32Yj t3)-f(ρ).(r21Xj r22Yj t2)＝0    (2.1) f(ρ).(r11Xj r12Yj t1)-uj.(r31Xj r32Yj t3)＝0    (2.2) uj.(r21Xj r22Yj t2)-vj.(r11Xj r12Yj t1)＝0    (2.3) 其中， Xj，Yj是已知的真实世界物理坐标，uj，vj是已知的图 像坐标，在公式(2.3)中H＝[r11，r12，r21，r22，t1，t2]为待求解参数，将L点坐标代入公式  (2.3)中得到方程组M·H＝0，其中 参数矩阵H的线性解采用最小二乘法||M·H||2，其中||H||2＝1，最后利用奇异值 分解计算出参数矩阵H；由于r1，r2，r3向量的正交性，能够计算出r31和r32。 进一步地，所述步骤2具体为： 在步骤1中根据公式(2.3)计算出摄像头的姿态参数，在此基础上根据公式(2.1) 和  (2.2)以及K组点来计算摄像头的内部结构参数及每组点所对应的t3；将K组点的坐标依 次代入公式(2.1)和(2.2)，得到如下方程： 其中， ， ， ， ； 由于方程(3)为线性方程组因此可以采用与步骤1相同的方法求解参数矩阵，至此 摄像头的姿态参数与内部结构参数均已求出。 进一步地，所述步骤3具体为： 建立优化目标函数将图像坐标转换成真实世界的物理坐标，并计算物理坐标的累 积误差；利用优化目标函数对各个参数求解偏导数并建立雅各比矩阵，所建立的优化目标 函数如公式(4)所示： 其中，E表示真实物理坐标与计算得到的物理坐标的累积误差，mij是真实的物理坐 标， 是通过公式(1)将图像坐标转换后的物理坐标，  R＝[r1  r2  r3]， 5 CN 111598954 A 说　明　书 3/5 页 通过公式(4)依次求解各个参数的偏导数得到雅各比矩阵，利用梯度下降优 化算法逐渐进行迭代，当连续迭代10次累积误差变化不超过  1％时停止迭代，非线性优化 完成，优化后的参数即是最终的参数。 附图说明 图1为本发明所述快速高精度摄像头参数计算方法的流程图。