技术摘要：
本发明提供一种深度学习与预测滤波结合的地震数据反假频插值方法，包括：根据仿真地震数据构造训练样本集和测试样本集；构建预测误差滤波器网络，所述预测误差滤波器网络包括深度学习以及预测滤波，其中，深度学习利用训练数据学习缺失的地震数据与非平稳预测滤波器之  全部
背景技术：
物理或经济上的限制使采集的地震信号通常存在地震道缺失或空间采样间隔过 大的问题，这将会影响后续的偏移成像、反演和解释。地震差值问题分为不规则缺失插值和 规则缺失插值，其中，规则缺失插值对数据进行上采样，是昂贵的密集空间采样的替代方 法，可以去除过大的空间采样间隔导致的频率混叠现象。 预测滤波是一类重要的地震数据反假频插值方法，例如f-x域反假频插值方法将 地震记录视为线性同相轴的叠加，从低频f估计的预测误差滤波器(PEF)可用于对高频2f的 数据进行插值，后来该方法被推广至t-x域、f-x-y域等。然而该方法基于线性同相轴假设， 而地震数据同相轴大多是非线性的，因此实际应用时要考虑加窗技术，以保证分析窗口中 的数据近似线性。非平稳的滤波器是另一种处理非线性同相轴数据的插值方法，非平稳滤 波器将滤波器系数的求解建模为欠定问题，通常需要引入正则化项来约束滤波器平滑变 化。 近年来，机器学习和深度学习技术为插值问题提供了新的思路，利用大数据的优 势可突破先验假设的限制，自动从数据中挖掘特征，极大地减少了人工工作量。例如，利用 支持向量回归(SVR)从训练数据中学习连续回归超平面，用以表示缺失数据与输出完整数 据之间的关系。深度学习是机器学习的子类，深层神经网络相比于SVR可以非线性地提取数 据更高层的特征，已有的研究包括使用残差网络对规则缺失数据插值、生成对抗网络对叠 后gap缺失数据插值、U-net网络对随机缺失数据插值等，这些方法构建不同的网络结构，从 大量的训练数据中学习退化数据(缺失或预插值)到完整数据的映射，训练好的网络能够直 接用于相似数据的插值，但难以学到一个对不同数据具有普适性的映射，同时由于深度网 络本身的不可解释性，这些方法的插值原理难以解释，插值效果也难以预估。
技术实现要素：
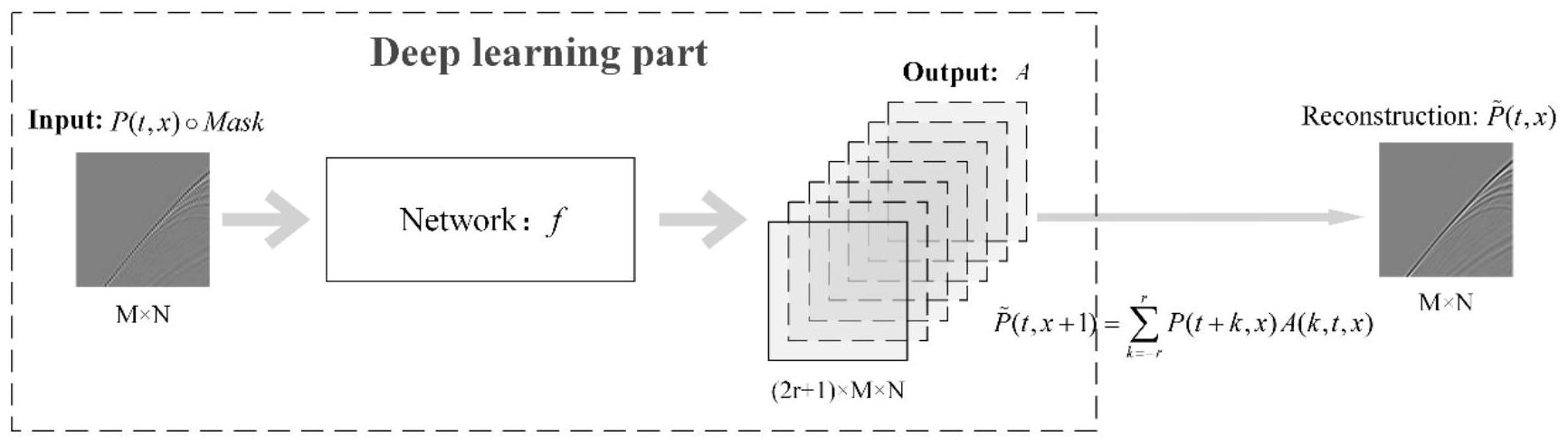
有鉴于此，本发明提供了一种深度学习与预测滤波结合的地震数据反假频插值方 法，考虑t-x域中的非平稳预测误差滤波器(Prediction  Error  Filter，PEF)，设计网络学 习退化数据和滤波器之间的关系，输入为缺失数据，输出为滤波器系数，然后使用该滤波器 重建缺失的地震道，本发明同时集成了深度学习和预测滤波方法的优点，能够有效地提取 地震数据的局部倾角特征，训练好的网络对不同类型的数据具有较好的适应性，计算效率 更高且测试阶段不需要人工调参。 本发明提供一种深度学习和预测滤波结合的地震数据反假频插值方法，包括以下 步骤： S1、对仿真地震数据进行不同尺度的空间下采样以扩充样本集，并从扩充后的样 4 CN 111551988 A 说　明　书 2/6 页 本集中随机截取若干M×N大小的数据块，然后将所述数据块分为训练样本集和测试样本 集，M表示数据块的行数，N表示数据块的列数； S2、构建预测误差滤波器网络，所述预测误差滤波器网络包括深度学习以及预测 滤波，其中，所述深度学习由残差网络实现，所述残差网络利用训练数据学习缺失的地震数 据与非平稳预测滤波器之间的映射关系；所述预测滤波利用学习得到的非平稳预测滤波器 对缺失的地震数据进行预测； S3、利用步骤S1中得到的训练样本集对预测误差滤波器网络进行训练，并利用测 试样本集评估所述预测误差滤波器网络的性能；利用训练完成后的预测误差滤波器网络对 地震数据进行反假频插值。 进一步地，所述步骤S1中不同尺度的空间下采样包括对仿真地震数据进行2倍下 采样和4倍下采样，且所述训练样本集和所述测试样本集截取自仿真地震数据的不同炮记 录。 进一步地，所述步骤S2中，所述残差网络的输入为规则缺失的地震数据 P(t,x)表示时间-空间域内完整的地震数据，t表示反射时间，x表示空间数 据，Mask表示用于构造规则缺失的地震数据的掩模算子，表示哈达玛积；所述残差网络的 输出为非平稳预测滤波器的系数A，系数A的矩阵大小为(2r 1)×M×N，r表示非平稳预测滤 波器的半径。 进一步地，所述步骤S2中，所述残差网络由7个残差块堆积而成，每个残差块均包 含两个卷积层，所述卷积层的卷积核大小为5×5，非线性激活函数采用Relu函数，并使用批 标准化层加速收敛；除第一层和最后一层的卷积层外，其余卷积层的输入和输出通道数均 为64；所述残差网络为一次下采样和一次上采样的编码解码结构，其中，所述下采样由步长 为2的卷积层实现，所述上采样由转置卷积实现。 进一步地，所述步骤S2中，所述预测滤波中利用学习得到的非平稳预测滤波器对 缺失的地震数据进行预测的具体过程为： 利用第x道地震数据对第x 1道地震数据进行预测： 其中， 表示时间t处第x 1道地震数据的预测结果，P(t k,x)表示时间t k 处第x道地震数据，A(k ,t ,x)表示(t,x)处的非平稳预测滤波器的第k个系数，k＝-r ,-r 1,…,r。 进一步地，所述步骤S3中，利用步骤S1中得到的训练样本集对预测误差滤波器网 络进行训练的具体过程为： 将训练样本集中原始完整的数据块作为标签数据Y，利用掩模算子Mask构造规则 缺失的地震数据 其中，X0为M×N的二维矩阵，然后将所述规则缺失的地 震数据X0归一化到[-1 ,1]之间得到数据X，从而构造训练样本对(X,Y)；所述归一化的方式 为X＝X0/max(|xi,j|)，X表示归一化后的地震数据，X0表示输入的规则缺失的地震数据，xi,j 表示X0中第i行第j列的元素，0＜i≤M，0＜j≤N，i、j为正整数。 进一步地，利用所述构造训练样本对(X,Y)对所述预测误差滤波器网络进行训练， 5 CN 111551988 A 说　明　书 3/6 页 具体过程为： 向残差网络中输入数据X，并根据残差网络输出的非平稳预测滤波器系数A对标签 数据Y进行一次预测，得到第1步预测的结果Y(1)： 其中，0＜i≤M，0＜j≤N，i、j为正整数，Y(1)中的第1至N-1列数据是对标签数据Y中 第2至N列数据的预测，A(k,i,j)表示(i,j)处的非平稳预测滤波器的第k个系数，k＝-r,-r 1,…,r； 根据非平稳预测滤波器的系数A对标签数据Y进行多步预测： 其中，Y(l 1)表示第l 1步预测结果，Y(l)表示第l步预测结果； 使用L1范数约束预测结果和标签数据Y的距离，由此得到损失函数： 其中，S表示最多预测的地震道的道数；使用adam梯度下降法优化损失函数，完成 对预测误差滤波器网络的一轮训练。所述adam梯度下降法的批尺寸为48，初始学习率为 0.001，且每5轮学习率乘以0.1，共训练15轮，完成对预测误差滤波器网络的训练。 进一步地，所述步骤S3中，利用测试样本集评估所述预测误差滤波器网络的性能 时，采用的评价指标为重建信噪比： 其中， 表示利用所述预测误差滤波器网络对测试样本集的中测试样本进行地震 数据插值的结果，Yt表示测试样本集中的标签数据， 表示F范数的平方。 本发明提供的技术方案带来的有益效果是：本发明同时集成了深度学习和预测滤 波方法的优点，相较于其他深度学习方法，具有更好的泛化性且滤波重建过程具有可解释 性，对不同数据自适应性更好；相较于传统预测滤波方法，可使用GPU并行计算，计算效率更 高，无需加窗策略和人工调参。 附图说明 图1是本发明实施例提供的训练样本集中的四个示例图； 图2是本发明实施例提供的预测误差滤波器网络的结构示意图； 图3是本发明实施例提供的残差网络的结构示意图； 图4是本发明实施例提供的规则缺失的地震数据的示意图； 图5是本发明实施例提供的PEFNet方法与ResNet、f-x、PWD方法的插值结果对比 图； 图6是本发明实施例提供的PEFNet方法对真实数据的插值结果的示意图。 6 CN 111551988 A 说　明　书 4/6 页