技术摘要：
本发明提供的分布式的关键型任务端到端时延优化方法及系统，该包括：根据端到端网络，构建底层核心网络的权重有向图；以链路拥塞因子作为优化变量，考虑链路存在故障时的链路‑路径流量恢复设计，构建时延优化模型；采用基于交替方向乘法子的Benders分解，对时延优化模  全部
背景技术：
随着网络技术的高速发展，5G通信网络需要严格保证物联网设备的QoS端到端服 务交付，则要求端到端服务交付更具有定制化以及延迟敏感的特性，并为物联网通信提供 更细粒度的服务质量。典型的物联网应用场景包括智能电网、大规模移动社交网络、工业自 动化与智能交通系统等。对于端到端服务交付，来自无线接入网络侧(RAN)的数据分组被聚 合在一起，并根据服务类型分组到业务流中，然后通过有回程链路将其转发到核心网络的 边缘路由器。 智能电网作为典型的垂直行业，多样化的电力业务所需的QoS要求也不同。智能电 网中一些时间关键的机器对机器通信业务，需要超高可靠性与低延迟的网络；实时控制类 与动态过程自动化调度等业务则需要这种时延能力极致的通信网络，可以将这些业务称为 电网中的关键任务通信。例如，面向低时延需求的配电自动化，通过检测配电网线路或设备 状态信息，可快速实现配网线路区段或配网设备的故障判断及准确定位，这在电力通信中 起着举足轻重的作用，其可靠性要求达到99.999％，同时需要高精度的时间同步需求以及 低时延需求，通信端到端传输时延要求小于10ms甚至更低。 端到端电力网络可以包括无线接入(RAN)部分与核心网络(CN)部分。在CN侧，使用 软件定义网络(SDN)和网络功能虚拟化(NFV)，可以使每个划分出的逻辑隔离的CN共享底层 网络基础设施(如路由、交换机与有线链路等)。同时，在核心网络中，VNFs可以被灵活地放 置在网络中，并且可以动态地请求和释放相应的资源。一组VNFs与连接它们的虚拟链路构 成逻辑VNF链，称为服务功能链(SFC)，表示业务流需要遍历以进行E2E服务供应的特定网络 功能序列。 面对不同种类的关键任务，服务于关键任务业务流的SFC将由不同设置在路由节 点上的VNFs构成。对于关键任务来讲，历经SFC的延迟敏感业务流的E2E分组延迟是指示切 片性能的主要度量。然而，关键任务通信仍然处于5G的早期标准化阶段，这带来了许多尚未 解决的研究问题。 在大多数现有的研究中，每个业务流的E2E分组延迟计算为每个物理链路上的分 组传输延迟的总和，而不考虑由于NFV节点上的CPU处理引起的分组处理延迟。因此，如何构 建一种分析模型来评估业务流历经SFC时的平均分组延迟，这是一项具有挑战性的工作，并 且对于实现SFC构成的时延感知的关键任务具有重要意义。
技术实现要素：
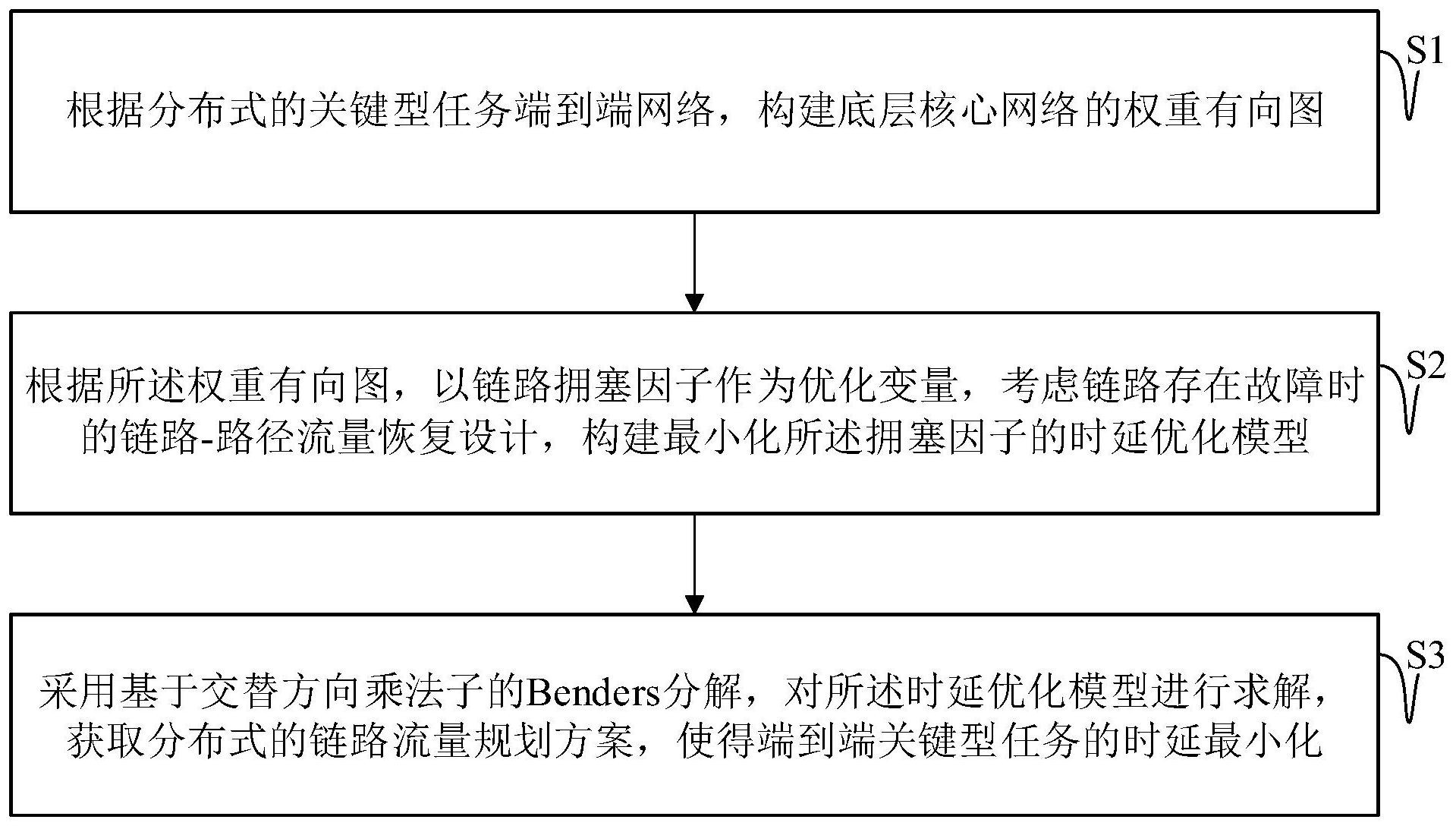
本发明实施例提供一种分布式的关键型任务端到端时延优化方法及系统，用以克 服现有技术在端到端时延优化计算时，是获取每个物理链路上的分组传输延迟，再计算传 8 CN 111614571 A 说　明　书 2/17 页 输延迟的总和，导致计算效率低、精算精度差，受制约条件多等缺陷。 第一方面，本发明实施例提供一种分布式的关键型任务端到端时延优化方法，主 要包括： S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；S2， 根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在故障时的链路-路径流量恢 复设计，构建最小化所述拥塞因子的时延优化模型；S3，采用基于交替方向乘法子的 Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到 端关键型任务的时延最小化。 作为可选地，上述S1，根据分布式的关键型任务端到端网络，构建底层核心网络的 权重有向图，可以包括： 确定关键型任务端到端网络的物理节点集合 链路集合ε、支持VNF功能的节点 的处理容量集合V以及链路容量集合C；根据物理节点集合、链路集合、支持VNF功能的节点 的处理容量集合以及链路容量集合，构建底层核心网络的权重有向图 作为可选地，上述根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在 故障时的链路-路径流量恢复设计，构建最小化所述拥塞因子的时延优化模型，其目标函数 为： 该时延优化模型的约束条件为： C1-1： C1-2： C1-3: C1-4: C1-5: C1-6: 其中，r为链路拥塞因子，e表示一条链路；p表示一条虚拟路径，h表示节点对之间 的需求量，d表示需求的编号，hd表示第d个业务的需求量；s表示链路e的故障状态，其中s＝ 0表示链路e正常运行，s＝e表示链路e发生故障； 为需求d可行的虚拟路径集合； 为业务 需求集合； 为链路状态集合；hd0表示正常状态下，第d个业务的需求量；hds表示在状态s 下，第d个业务的需求量；xdp0表示正常状况下，需求d在虚拟路径p上的流量；xdps表示在状态 s下，需求d在虚拟路径p上的流量；δedp为作为路径-链路指示记号的二值常量，对于需求d， 9 CN 111614571 A 说　明　书 3/17 页 如果链路e在虚拟路径p上，则δedp＝1，否则为δedp＝0；udp0为指示在正常状况下需求d是否使 用虚拟路径p的二元变量，若使用虚拟路径p，则udp0＝1，否则均udp0＝0；udps为指示在状态s 下需求d是否使用虚拟路径p的二元变量，若使用虚拟路径p，则udps＝1，否则均udps＝0；θdps 为指示需求d的虚拟路径p在状态s下可用性的二元常量；xdps为需求d的虚拟路径p在状态s 下的恢复流变量；xdp0为需求d的虚拟路径p在正常状况下的恢复流变量；ye为链路e上的负 载；αes为表示链路e是否处于故障状态s的二元常量。 作为可选地，上述S3，采用基于交替方向乘子法的Benders分解，对时延优化模型 进行求解，可以包括以下步骤： S3.1，基于Benders分解，将对时延优化模型的分解为一个首问题模型P2和一个主 问题模型P6； S3.2，对首问题模型P2进行可行性检验； S3.3，若首问题模型P2可行，基于交替方向乘子法对首问题模型进行P2求解，获取 到拉格朗日乘子最优割和上界信息，将拉格朗日乘子最优割反馈至主问题模型P6； S3.4，基于分支定界法，根据拉格朗日乘子最优割，对主问题模型P6进行求解，以 更新首问题模型P2的二元变量udp0、udps，并获取下界信息； S3.5，迭代执行S3.2-S3.4，直至判断首问题模型P2不可行，获取每条链路负载以 及每条虚拟路径的流变量，以确定分布式的链路-路径流量规划方案。 作为可选地，上述S3.1，基于Benders分解，将对时延优化模型的分解为一个首问 题模型P2和一个主问题模型P6，可以包括以下步骤： 在确定第v次迭代时候的二元变量udp0和udps之后，根据时延优化模型获取首问题 模型P2；首问题模型P2的目标函数为： 首问题模型P2的约束条件为： C2-1: C2-2: C2-3: C2-4: 主问题模型P6的目标函数为： 主问题模型P6的约束条件为： C6-1: C6-2: 10 CN 111614571 A 说　明　书 4/17 页 C6-3: C6-4: 其中，V1 V2＝v，v为总迭代次数，V1为当首问题可行时，解决首问题的迭代次数；V2 为当首问题不可行时，解决l1-min问题时的迭代次数； 分别为第V1次迭代时需求d的虚 拟路径p在状态s下的恢复流变量； 为第V1次迭代时链路e上的负载； 为第V1次迭代时 的拉格朗日乘子； 为拉格朗日乘子最优割时的拉格朗日函数； 和 分别为与 所述拉格朗日乘子最优割对应的第V2次迭代时需求d的虚拟路径p在状态s下的恢复流变 量、链路e上的负载以及拉格朗日乘子。 作为可选地，上述S3.3，若首问题模型P2可行，基于交替方向乘子法对所述首问题 模型P2进行求解，具体包括以下步骤： S3.3.1，获取首问题模型P2的拉格朗日函数 其中，λ＝(λ1,λ2,λ3,λ4)为拉格朗日乘子， 为第V次迭代时指示在状态s下需求d 是否使用虚拟路径p的二元变量； 为第V次迭代时指示在正常状态下需求d是否使用虚拟 路径p的二元变量； S3.3.2，基于拉格朗日函数 获取首问题模型P2的对偶模型P2-Dual：对 偶模型P2-Dual的目标函数为： 对偶模型P2-Dual的约束条件为： λ≥0； S3.3.3，将对偶模型P2-Dual分解为内层最小化模型P3和外层最大化模型P4，内层 最小化模型的求解变量为二元变量xdps、ye，外层最大化模型的求解变量为拉格朗日乘子λ ＝(λ1,λ2,λ3,λ4)； 内层最小化模型P3为无约束模型，其目标函数为： 外层最大化模型P4的目标函数为： 11 CN 111614571 A 说　明　书 5/17 页 外层最大化模型P4的约束条件为： λ≥0； 其中， 分别是在内层优化中获取的每条链路负载以及每条虚拟路径的流 变量的最优解； S3.3.4，基于交替方向乘子法对所述内层最小化模型P3求解； S3.3.5，对首问题模型P2中的拉格朗日乘子进行更新，完成对外层最大化模型P4 进行求解。 作为可选地，上述S3.3.4，基于交替方向乘子法对内层最小化模型P3求解，包括单 不限于以下步骤： 引入辅助变量fe作为链路e上的负载变量ye的复制，获取首问题模型P2的增广拉格 朗日函数 其中，μe是对应这个等式约束的拉格朗日乘子，ρ是惩罚参数；E为链路总数； 获取转换后的内层最小化模型P3’： 其中，变量ye，fe，xdps和乘子μe的更新方式分别如下： μe[t 1]＝μe[t] ρ(fe-ye) 其中，t为当前更新次数。 作为可选地，在上述S3.3.5，对所述首问题模型P2中的拉格朗日乘子进行更新，完 成对所述外层最大化模型P4进行求解中，所述拉格朗日乘子更新的步骤为： 其中， 为第o次迭代时候的步长，i为更新的次数，运算符[x] ＝max{0,x}。 作为可选地，在所述S3.5中，直至判断所述首问题模型P2不可行，获取每条链路负 载以及每条虚拟路径的流变量，包括： 若判断首问题模型P2不可行，则创建可行割确定模型l1-min； 可行割确定模型l1-min的目标函数为： 12 CN 111614571 A 说　明　书 6/17 页 可行割确定模型l1-min的约束条件为： C5-1: C5-2: C5-3: C5-4: 其中，qj为新引入的约束破坏变量，所述约束破坏变量用于当无可行解满足首问 题时，松弛对首问题的约束条件。 根据可行割确定模型l1-min，获取拉格朗日乘子最优割 其中， 是与qj相对应的拉格朗日乘子； 根据拉格朗日乘子最优割 确定当前每条链路负载以及每条虚拟路 径的流变量。 第二方面，本发明实施例提供一种分布式的关键型任务端到端时延优化系统，主 要包括：拓扑结构构建单元、时延优化模型单元和模型运算单元，其中： 拓扑结构构建单元主要用于根据分布式的关键型任务端到端网络，构建底层核心 网络的权重有向图；时延优化模型单元，用于根据所述权重有向图，以链路拥塞因子作为优 化变量，构建最小化拥塞因子的时延优化模型；模型运算单元主要用于采用基于交替方向 乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案， 使得端到端关键型任务的时延最小化。 第三方面，本发明实施例提供一种电子设备，包括存储器、处理器及存储在存储器 上并可在处理器上运行的计算机程序，其中，处理器执行所述程序时实现如第一方面任一 所述的分布式的关键型任务端到端时延优化方法的步骤。 第四方面，本发明实施例提供一种非暂态计算机可读存储介质，其上存储有计算 机程序，该计算机程序被处理器执行时实现如第一方面任一所述的分布式的关键型任务端 到端时延优化方法的步骤。 本发明实施例提供的分布式的关键型任务端到端时延优化方法及系统，采用简洁 13 CN 111614571 A 说　明　书 7/17 页 的方法对底层核心网络进行设计，创建了一个针对最小化最大链路拥塞因子的问题模型， 并采用基于交替方向乘法子的Benders分解对该模型进行求解，以得到分布式的链路-路径 流量规划方案，使得端到端关键型任务时延最小化，兼顾了链路-路径的流量恢复设计，有 效的提高了优化的效率和精度。 附图说明 为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现 有技术描述中所需要使用的附图作一简单地介绍，显而易见地，下面描述中的附图是本发 明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根 据这些附图获得其他的附图。 图1为本发明实施例提供的一种分布式的关键型任务端到端时延优化方法流程示 意图； 图2为本发明实施例提供的一种分布式的关键型任务端到端网络构架示意图； 图3为本发明实施例提供的一种底层网络模型示意图； 图4为现有技术中的一种平均时延和链路利用率曲线示意图； 图5为本发明实施例提供的一种分布式的关键型任务端到端时延优化方法的框架 图； 图6为本发明实施例提供的一种ADMM实施方法的模型示意图； 图7为本发明实施例提供的一种分布式的关键型任务端到端时延优化系统的结构 示意图； 图8为本发明实施例提供的一种电子设备的实体结构图。