技术摘要：
本发明公开了一种基于贝叶斯学习的执行器故障估计方法，包括(1)基于随机走步模型对执行器故障建模；(2)基于变分贝叶斯理论，将系统状态变量和执行器故障信号的联合后验分布用两个相互独立的假设分布来表示；(3)在k‑1时刻，预测出k时刻系统的状态和故障；在k时刻，依据  全部
背景技术：
执行器作为控制回路重要的一部分，其运行的健康程度决定着回路的控制效果， 继而影响整个控制过程的安全性与可靠性。因此，针对控制回路执行器的故障诊断十分重 要。目前，在许多国际刊物上均报道了控制回路中执行器故障诊断的方法。例如，Alrowaie 等人在多模型结构下利用粒子滤波对非线性状态空间下的故障信号进行检测与隔离， (F.Alrowaie,R.B.Gopaluni,K.E.Kwok,Control  Engineering  Practice,2012,20:1016- 1032) .Zhong等人设计了针对线性离散时变系统的最优故障诊断算法(M.Zhong ,S.Ding , E.Ding,Automatica,2010,46:1395-1400)。He等通过去噪和趋势分离等手段设计了针对微 小执行器故障的算法(Z .He ,Yuri ,Shardt ,D .Wang ,B .Hou ,H .Zhou ,J .Wang ,Control  Engineering  Practice,2018,74:1-12)。Nguyen等提出了利用滑膜观测器来对执行器故障 进行估计(N.P.Nguyen,N.X.Mung,S.K.Hong,Sensors,19(21):4721.)Zhang等设计了针对 柴油引擎故障的自适应滑膜观测器(H .Zhang ,J .Wang ,IEEE/ASME  Transactions  Mechatronics,21(4):2027-2038。Ding在其书中对现有基于模型的故障诊断技术做了详细 的论述(S.X.Ding,NewYork,NY,USA:Springer,2013) . 然而，上述方法主要针对执行器故障的诊断问题，没有考虑执行器故障信号的估 计问题。已知，故障估计的重要性往往高于故障诊断，其主要原因在于故障估计不仅可以提 供故障发生的时间、故障大小，还能给出故障信号发生的位置及故障性质。目前只有在确定 性系统中有针对执行器故障的估计方法，而实际过程中，由于工作环境、设备老化、人为等 因素，控制回路往往表现出较强的随机性，随机系统十分常见，而目前没有针对随机系统的 执行器故障估计方法。
技术实现要素：
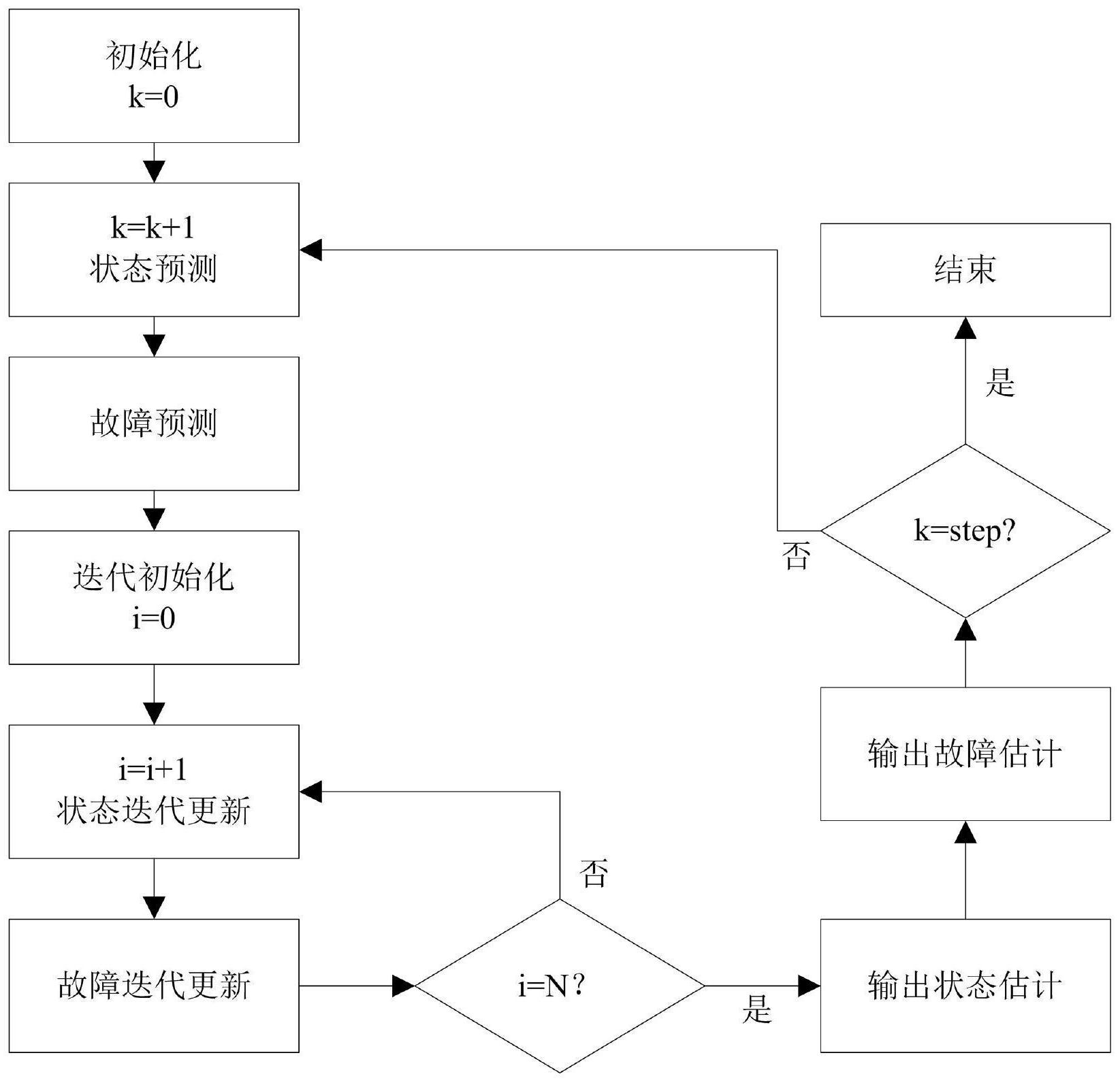
本发明要解决的技术问题是提供一种基于贝叶斯学习的执行器故障估计方法，该 估计方法针对随机系统下执行器故障适用，能够很好地对执行器故障信号进行估计，弥补 现有方法在这一方向的缺失。 为了解决上述技术问题，本发明提供了一种基于贝叶斯学习的执行器故障估计方 法，包括以下步骤， (1)基于随机走步模型对执行器故障建模如下， fk为k时刻潜在的执行器故障信号；fk-1为k-1时刻潜在的执行器故障信号； 为白 噪声，服从高斯分布 为已知的噪声方差；k为时间序列； 表征均 5 CN 111611718 A 说　明　书 2/7 页 值为零，方差为 的高斯分布； (2)基于变分贝叶斯理论，将系统状态变量和执行器故障信号的联合后验分布p (xk,fk|y1:k)用两个相互独立的假设分布q(xk|y1:k)和q(fk|y1:k)来表示，即 p(xk,fk|y1:k)＝q(xk|y1:k)q(fk|y1:k)   (式2)； 在k-1时刻，将状态和故障信号的联合概率分布按照如下方式近似： y1:k＝{y1，y2，…，yk}表示从1时刻到k时刻观测信号的合集；xk为k时刻系统状态变 量； 表示系统状态在k-1时刻的均值；Pk-1为 方差； 为故障信号在k-1的估计值； Δk-1为 方差； (3)在k-1时刻，预测出k时刻系统的状态和故障；在k时刻，依据贝叶斯理论对预测 出的系统状态和系统故障进行迭代更新，输出k时刻系统状态的估计值和该估计值的方差， 以及输出k时刻系统故障的估计值和该估计值的方差。 本发明一个较佳实施例中，进一步包括步骤(3)中，将k-1时刻的预测值作为k时刻 迭代更新的初始值，即 和 这里，i表示迭代步数， 其最大迭代步数设为N；其中， 为k时刻状态预测值， 为k时刻状态预测的方差， 为k时 刻故障预测值， 为k时刻故障预测的方差，Θ＝τI,I为单位矩阵，τ∈(0，1]为可调参数。 本发明一个较佳实施例中，进一步包括步骤(3)中，根据执行器所在控制回路的动 态模型方程，在k-1时刻预测出k时刻的系统状态和方差， 为k时刻状态预测； 为k时刻状态预测的方差； 为k-1时刻状态预测值； 为故障信号在k-1时刻的估计值；uk-1为控制回路的控制器输出；Pk-1为k-1时刻状态方差预 测值；Δk-1为 方差；Qk为系统状态方差；A为状态转移矩阵；B为控制器输入矩阵。 本发明一个较佳实施例中，进一步包括依据贝叶斯理论对预测出的k时刻系统状 态和方差进行迭代更新，具体步骤为， 为k时刻第i次迭代的系统状态估计值； 为k时刻状态预测； 为第i-1迭代次 数下故障信号的估计值；i表示迭代步数，其最大迭代步数设为N；K为控制回路中滤波器增 益；yk为k时刻系统状态的观测值；C为状态的观测矩阵； 为k时刻第i次迭代的状态估计方 6 CN 111611718 A 说　明　书 3/7 页 差； 为k时刻状态估计方差的预测值；Rk为观测噪声的方差。 本发明一个较佳实施例中，进一步包括步骤(3)中，输出k时刻系统状态的估计值 及其方差为： 为k时刻系统状态的估计值；Pk为k时刻系统状态的方差。 本发明一个较佳实施例中，进一步包括步骤(3)中，根据执行器故障动态方程，在 k-1时刻预测出k时刻系统的故障和方差， 为k时刻故障预测值； 为k时刻故障预测的方差； 为故障信号在k-1时刻的 估计值；Δk-1为 方差；Θ＝τI,I为单位矩阵；τ∈(0，1]为可调参数。 本发明一个较佳实施例中，进一步包括依据贝叶斯理论对预测出的k时刻系统故 障和方差进行迭代更新，具体步骤为， 为k时刻第i次迭代的故障信号的估计值； 为k时刻故障信号的预测值； 为 k时刻故障信号的预测方差； 为k时刻系统状态方差； 为k时刻第i次迭代的系统状态的 估计值； 为k-1时刻系统状态的估计值； 为k时刻第i次迭代的故障信号的方差。 本发明一个较佳实施例中，进一步包括步骤(3)中，输出k时刻系统故障的估计值 fk及其方差Δk： 本发明一个较佳实施例中，进一步包括所述估计方法还包括，建立包含执行器故 障信号的开环控制回路动态模型和观测动态模型，并对获得的观测数据使用3δ准则进行预 处理，所述预处理包括剔除奇异值。 本发明一个较佳实施例中，进一步包括所述估计方法还包括，输出k时刻系统状态 和系统故障后，判断是否满足k＝step，是则结束；否则k＝k 1，并跳转至第(2)步；step为最 大时间长度。 本发明的有益效果： 本发明基于贝叶斯学习的执行器故障估计方法，该估计方法针对随机系统下执行 器故障适用，能够很好地对执行器故障信号进行估计，弥补现有方法在这一方向的缺失，具 体表现在：基于随机走步模型对执行器故障信号进行建模，利用贝叶斯学习算法在线学习 7 CN 111611718 A 说　明　书 4/7 页 得到系统状态和故障信号的实时估计值，通过故障信号的估计值，可以直观判断出执行器 所在控制回路当前是否存在故障。若存在故障，通过本发明的估计方法也可以直观地得到 当前故障的发生时间、当前故障值，以及当前故障发生在哪个状态变量上。 附图说明 图1为执行器所在控制回路的开环结构图； 图2为本发明优选实施例中执行器故障估计方法的流程图； 图3为使用本发明估计方法对两类方形波的故障信号估计效果图； 图4为使用本发明估计方法对三角函数波形的故障信号估计效果图。