技术摘要：
本发明公开了一种城市环境下协同探测系统的目标分配优化方法，能够在综合考虑低慢小目标的特性以及城市环境中的障碍与资源的影响下，解决传感器网络的目标分配优化问题。具体为：n个目标接近时，协同探测系统中的探测节点对威胁目标进行探测识别，得到目标检测状态影响  全部
背景技术：
低慢小目标是具有低空或超低空飞行、速度较慢、不易被侦察发现等特征的各种 小型航空器和空漂物的统称。由于成本低廉、操控简单、携行方便，它易于被极端用户和恐 怖分子利用，产生不可估量的后果。 为了对低慢小目标进行系统化的防控，低慢小目标防控指挥控制系统应运而生。 指挥控制系统首先通过探测系统获取目标的状态信息，对目标信息进行融合，从而获取目 标的准确信息，再对目标进行评估排序，指示探测装备对目标进行跟踪，必要情况下控制拦 截系统进行火力分配，对目标进行捕获拦截。由于探测系统的节点数量和种类众多，城市环 境中也往往同时存在多个低慢小目标，如何有效对协同探测系统的目标进行有效分配是其 中的重点难题。 探测系统的目标分配，旨在解决有限探测资源的情况下，监控区域内出现多个威 胁目标时，如何确定多个探测装备对多个目标的最佳配对，使得探测系统的综合监测能力 最优，该问题本质上属于资源受限的规划问题。目标分配通常需要解决两个问题，一是建立 一个科学合理又切实可行的包含目标函数和约束条件的分配模型，二是设计一个流程准确 又高效可行的求解算法。 在国内外已有的研究成果中，对目标分配建模的方法，目前主要有以下几类：基于 线性规划的方法、基于动态规划的方法、基于协方差控制的方法。 根据国内外文献调研的结果，虽然当前的目标分配问题的方法已经相对成熟，在 对具体环境中的目标分配问题建模时往往趋于简化，而在复杂环境中这种简化导致模型可 靠性较差。在已有的国内外成果中，往往以空旷开阔区域为场景，对障碍物的影响因素考虑 不足，而城市环境中遮挡较多。城市环境限制了探测节点的跟踪半径，因而单个探测节点在 模糊半径范围内的跟踪精度很低，因而目标最好由多个探测节点跟踪，此时探测节点对目 标的跟踪的有效距离应该综合考虑。另外传统空中目标跟踪过程中很少有目标静止的情 况，而低慢小目标由于目标速度本身较低，而且多旋翼类型的无人机由于自身设计的原因， 可以做到悬停一段时间，因而需要考虑目标静止的情况。而且低慢小目标机动性较强，可以 较快地调整飞行方向，在评价低慢小目标的优先级时不仅需要考虑目标当前飞行方向上的 威胁，更需要对所有方向的潜在威胁进行分析。 关于目标分配模型的求解，粒子群算法PSO作为一种高效的智能优化算法，常被用 在目标分配问题上。但是标准PSO算法是用于连续空间的，而探测节点和目标间的分配问题 取值都是离散化的，因此首先需要对PSO算法进行离散化。而且标准粒子群算法中粒子的每 一维元素都在变化，可能存在一些维度的元素靠近最优位置而其他维上的元素远离最优位 置，从而导致出现粒子的适应度比上一代差的情况，造成PSO算法陷入局部最优。 6 CN 111553601 A 说　明　书 2/16 页 综上，如何综合考虑低慢小目标的特性以及城市环境中的障碍与资源的影响，建 立优化分配模型，对PSO算法进行优化并求解模型，是一个有待解决的新问题。
技术实现要素：
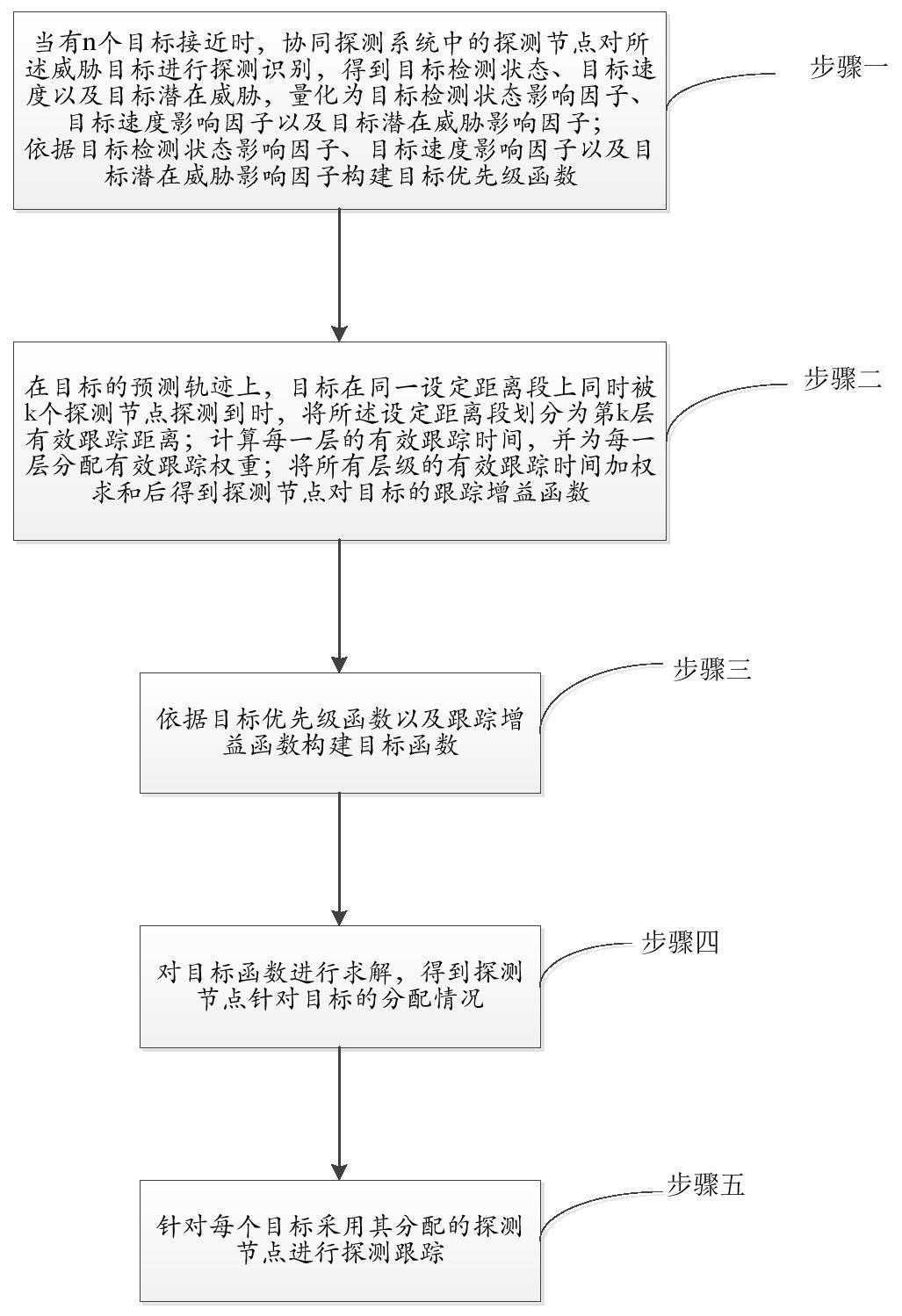
有鉴于此，本发明提供了一种城市环境下协同探测系统的目标分配优化方法，是 一种面向城市环境的协同探测系统的目标分配优化模型和优化策略，在综合考虑低慢小目 标的特性以及城市环境中的障碍与资源的影响下，解决传感器网络的目标分配优化问题。 为达到上述目的，本发明的技术方案一种城市环境下协同探测系统的目标分配优 化方法，所针对目标为低慢小飞行器，包括如下步骤： 步骤一、当有n个目标接近时，协同探测系统中的探测节点对威胁目标进行探测识 别，得到目标检测状态、目标速度以及目标潜在威胁，量化为目标检测状态影响因子、目标 速度影响因子以及目标潜在威胁影响因子； 依据目标检测状态影响因子、目标速度影响因子以及目标潜在威胁影响因子构建 目标优先级函数。 步骤二、在目标的预测轨迹上，目标在同一设定距离段上同时被k个探测节点探测 到时，将设定距离段划分为第k层有效跟踪距离；k为正整数； 计算每一层的有效跟踪时间，并为每一层分配有效跟踪权重；将所有层级的有效 跟踪时间加权求和后得到探测节点对目标的跟踪增益函数。 步骤三、依据目标优先级函数以及跟踪增益函数构建目标函数。 设定约束条件包括：一个探测节点所分配的跟踪目标数目不超过其最大跟踪能 力；以及、任一目标分配不超过设定数量的探测节点。 步骤四、对目标函数进行求解，得到探测节点针对目标的分配情况。 步骤五、针对每个目标采用其分配的探测节点进行探测跟踪。 进一步地，协同探测系统中的探测节点对威胁目标进行探测识别，得到目标检测 状态、目标速度以及目标潜在威胁，量化为目标检测状态影响因子、目标速度影响因子以及 目标潜在威胁影响因子。 具体为： 目标检测状态包括识别状态和注册状态；识别状态即目标能否被成功识别；注册 状态即目标是否为被注册登记过的飞行器； 对于第j个目标，设定其目标检测状态影响因子为fst(j)： 其中fid(j)＝1表示目标为被注册登记过的飞行器；freg(j)＝1表示目标能够被成 功识别。 第j个目标的速度影响因子为fv(j)： 其中，m1、n1为依经验设定的调整系数；vx(j)、vy(j)、vz(j)为第j个目标的速度在城 市空间坐标系oxyz中x、y、z轴的分量；城市空间坐标系为以城市中心为原点o，以北向为x 7 CN 111553601 A 说　明　书 3/16 页 轴，东向为y轴，纵向为z轴。 第j个目标的潜在威胁影响因子为fthreat(j)： 其中取潜在威胁的方向为φ∈{0,φd,2φd,…,2π}，第j个目标与φ方向的最近建 筑物的距离为fd(j,φ)；φd为依经验设定的方向间隔。 fθ(j,φ)为第j个目标切换到φ方向的调整难度，fθ(j,φ)＝1-|φ-π|/π； fg(j,φ)为第j个目标在φ方向上运动的对地速度范围。 fg(j,φ)＝vgmax(j,φ)-vgmin(j,φ)； vgmax(j,φ)为第j个目标在φ方向上运动的对地速度最大值，vgmin(j,φ)为第j个 目标在φ方向上运动的对地速度最小值。 依据目标检测状态影响因子、目标速度影响因子以及目标潜在威胁影响因子构建 目标优先级函数，具体为： 第j个目标的优先级函数为L(j)＝fst(j)×fv(j)×fthreat(j)。 进一步地，计算每一层的有效跟踪时间，并为每一层分配有效跟踪权重；将所有层 级的有效跟踪时间加权求和后得到探测节点对目标的跟踪增益函数。 具体为： 第i个探测节点针对第j个目标在第k层的有效跟踪时间为gvt(i,j,k)； 其中，Vd(i,j,k)第i个探测节点针对第j个目标在第k层的有效跟踪距离； 为第i 个探测节点的最大探测半径； 是探测节点的隶属度函数，表示了不同类型探测节点 的识别准确性在不同气象环境W下的衰减程度；vj为第j个目标的速度。 第i个探测节点针对第j个目标在第k层的有效跟踪权重为gvw(i,j,k)： 其中wp(q)为第i个探测节点针对第j个目标在第k层的有效跟踪距离内点q的权 重，其中q为Vd(i,j,k)第i个探测节点针对第j个目标在第k层的有效跟踪距离内任一点。 第i个探测节点对第j个目标的跟踪增益函数为g(i,j)。 m2为依经验设定的调整系数。 进一步地，依据目标优先级函数以及跟踪增益函数构建目标函数，设定约束条件 包括：一个探测节点所分配的跟踪目标数目不超过其最大跟踪能力；以及、任一目标分配不 超过设定数量的探测节点；具体为： 8 CN 111553601 A 说　明　书 4/16 页 目标函数为Jtr： 其中设定分配矩阵为r(i,j)，M为探测节点总数，N为目标总数，r(i,j)包括M行N 列，r(i,j)为分配矩阵，行为每个探测节点，列为各目标，第i行第j列的值为rij，rij表示第i 个探测节点对第j个目标的探测识别能力，若第i个探测节点能够探测识别第j个目标则rij ＝1，否则rij＝0；f(j)表示在以r(i,j)矩阵作为分配分案的基础上，是否能对第j个目标跟 踪，f(j)＝1表示可以对第j个目标进行跟踪，f(j)＝0表示无法对第j个目标进行跟踪。 设定约束条件包括：一个探测节点所分配的跟踪目标数目不超过其最大跟踪能 力： Ci为第i个探测节点的最大跟踪能力。 任一目标分配不超过设定数量的探测节点；设定数量为Ntmax： 进一步地，对目标函数进行求解，得到探测节点针对目标的分配情况，具体为： 构建目标分配优化方程： 采用基于遗传算子的模拟退火PSO算法对目标分配优化方程进行求解，得到矩阵r (i,j)的解，从而得到探测节点针对目标的分配情况。 进一步地，采用基于遗传算子的模拟退火PSO算法对目标分配优化方程进行求解， 具体包括如下步骤： 1)初始化粒子群，即产生初始种群，设定迭代次数，其中需要对PSO算法进行离散 化，为了减少算法维度，采用整数法进行编码，建立粒子在第j维取值范围[1,2,...,Kj]和 探测节点排列组合方式之间的双重映射，取值范围如下： 其中Kj为粒子在第j维的取值范围；Ntmax为一个探测目标最多可以分配的探测节点 数量；Nj为可以探测到目标j的探测节点数量；j为探测目标编号；n为取值从1到m的整数；m 为取值从1取到Ntmax的整数。 9 CN 111553601 A 说　明　书 5/16 页 2)计算种群的适应度值，根据所建立的模型，由于第二个约束条件已经考虑在编 码过程中，迭代过程中只需要判断第一个约束条件即可，规定适应度如下： 其中sgn为符号函数；L(j)为第j个目标的优先级函数；f(j)表示在以r(i,j)矩阵 作为分配分案的基础上，是否能对第j个目标跟踪；r(i,j)为分配矩阵；g(i,j)第i个探测节 点对第j个目标的跟踪增益函数；Ci为第i个探测节点的最大跟踪能力。 该适应度函数将约束条件作为影响因素，使违反约束条件的解适应度值足够小， 基本不可能成为最优解，保证最终求得的解满足约束条件。 3)根据步骤二所计算的适应度值，更新粒子的局部最优和全局最优，并对每个粒 子进行速度更新和位置更新，利用随机游走项来替换传统速度更新公式中的一次速度项， 速度更新公式为： v(t 1)＝c0×r0 c1×r1×(pbest(t)-x(t)) c2×r2×(gbest(t)-x(t))     (18) 其中，c0是扰动的幅度，r0～U(0,1)是均值为0、标准差为1的标准正态分布；v(t)表 示粒子第t次迭代的速度，x(t)表示粒子第t次迭代的位置，r1和r2是0到1之间均匀分布的随 机变量，pbest为该粒子的历史最优解，gbest为当前种群的全局最优解；c1和c2分别为“认知 因子”和“社会因子”，用于控制粒子向其个体最优位置和全局最优位置运动的程度。 4)对种群粒子进行交叉和变异，所有粒子均与最优粒子进行交叉，在交叉过程中 依然要限制粒子的位置，之后对粒子进行变异，之后重新对粒子适应度值进行计算，根据与 前代的适应度值之差，确定是否接受新的解。 5)返回第二步，迭代进行到最大迭代次数后停止。 有益效果： 本发明提出的一种城市环境下协同探测系统的目标分配优化方法，引入了分层有 效跟踪距离的概念，建立了目标优先级评价的指标体系，考虑了不同探测节点相互间的协 同跟踪能力，并考虑了城市气象环境因素，使得所建立的模型更符合具体城市环境，可靠性 更高。而且，本发明在标准PSO算法的基础上根据模型特点进行改进，形成改进的PSO算法， 方针证明，在建立的模型中，该算法有效搜索效率，有效避免了传统PSO算法易陷入局部最 优的情况。，在不同目标数量、不同气象环境中，相比标准PSO和GAPSO算法，改进的PSO算法 不仅最终能够寻找到更优的解，还能在较少的迭代次数里找到更好的解。 附图说明 图1为本发明实施例中涉及的事件触发时序图； 图2为本发明实施例中涉及的探测节点和目标分配示意图； 图3为本发明实施例中涉及的评价指标层次结构图； 图4为本发明实施例中涉及的探测节点对目标的有效跟踪距离示意图； 图5为本发明实施例中涉及的探测节点对目标的多层有效跟踪距离示意图； 图6为本发明实施例中涉及的标准PSO算法流程图； 图7为本发明实施例中涉及的改进后GSAPSO算法的伪代码图； 10 CN 111553601 A 说　明　书 6/16 页 图8为本发明实施例中涉及的目标分配算法比较图； 图9为使用最优Pareto算法计算探测节点，得到探测节点的部署结果的俯视图； 图10为不同算法迭代过程比较图； 图11为本发明实施例提供的一种城市环境下协同探测系统的目标分配优化方法 流程图。