技术摘要：
本发明提供了基于串行式融合的GA&PSO优化算法研究。针对遗传算法操作盲目、无方向性、计算时间长、精度不高和粒子群算法的种群多样性差，易出现早熟从而陷入局部最优等单一算法的缺点，本发明采用串行式的算法融合思想，将一个算法进化得出的种群作为另一个算法执行的  全部
背景技术：
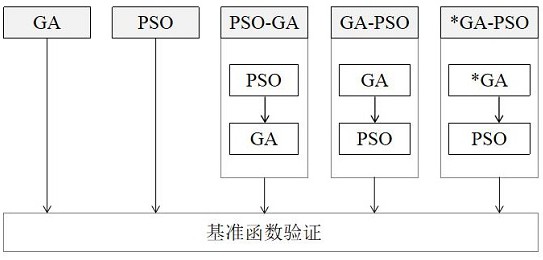
遗传算法(GA)由美国Holland教授基于生物界优胜劣汰的自然选择现象于1975年 提出用于解决优化问题，又称进化算法。遗传算法使用群体搜索技术，其所操作的对象以及 问题的解均为种群。通过对当前种群施加一系列遗传操作来产生新一代种群，包括优选强 势个体的选择、个体间交换基因片段产生新个体的交叉以及某位基因信息突变而产生新个 体的变异等。以此逐步迭代进化直到产生最优解。其过程简单，多用于函数优化，数据挖掘， 图像处理等。但有局限性，例如在多约束条件下收敛速度减慢，收敛精度不高等。 粒子群算法(PSO)是一种通过对鸟类觅食过程的模拟进行优化的算法。粒子群算 法中的每个粒子肩负两个值：位置和速度。粒子的位置表征可行解，速度用来决定粒子的运 动方向和距离。此外所有粒子通过跟踪自身经验极值和全局极值来更新自己的位置和速 度。其原理简单，用速度位移公式迭代即可实现，此外需调节的参数较少，粒子也具有记忆 性，多用于组合优化，传感器网络，车辆调度等。但随着智能优化算法的不断完善，其易陷入 局部最优，难处理多维问题的缺点也暴露出来。 单一智能优化算法已经不能满足当下出现的大规模、多变量、多约束、多极化及非 线性等复杂的问题，智能算法融合应运而生。近年来，已有多位学者将其融合，主要形式有 三种，第一，并行式混合，如Benvidi  A等提出用GA-PSO并行混合优化ANN参数，而且利用该 算法处理了吸光度数据和分析物浓度的关系，取得很好效果；第二，嵌入式混合，如孙丽平 将GA嵌入PSO中用于改进蒙特卡罗滤波和递推贝叶斯理滤波结合的粒子滤波样本退化问 题，并且实验证明了有效性；第三，串行式混合，如Zhang  J等提出在GA算法完成后叠加PSO 来实现聚类，效果虽实现了，但依旧存在收敛速度慢等问题。
技术实现要素：
针对遗传算法操作盲目、无方向性、计算时间长、精度不高和粒子群算法的种群多 样性差，易出现早熟从而陷入局部最优等单一算法的缺点，本发明提供了基于串行式融合 的GA&PSO优化算法研究，串行式融合算法相对于单一算法在计算精度、收敛速度、全局稳定 性方面均有明显提升；此外针对已有串行式融合研究存在的收敛速度慢的问题，本发明还 提供了改进GA-PSO，在保证计算精度的基础上，明显提高了收敛速度。 本发明提供基于串行式融合的GA&PSO优化算法研究，其技术方案如下。 采用串行式的算法融合思想，将一个算法进化得出的种群作为另一个算法执行的 初始种群，即GA-PSO或PSO-GA。即需要先单独执行GA和PSO，而后将GA算法进化得出的种群 作为PSO算法执行的初始种群，或将PSO算法迭代出的最优结果作为GA算法的初始种群。另 外还提出一种改进GA-PSO，随机初始化的粒子群个体经改进GA优化一遍直接交由PSO执行。 5 CN 111598209 A 说　明　书 2/10 页 最后利用基准函数来验证各算法的性能。 单独执行GA算法包括如下步骤。 (1)变量初始化： 群体规模太小不利于遗传性能的提升，规模大可减小其陷入局部最优但意味着复杂度 提升，故设染色体数目NP=100。每条染色体上的基因数D=10，最大遗传代数G=1000，交叉概 率太大虽可增强搜索新区域的能力但高性能模式易被破坏故设Pc=0.8，而变异在整个遗传 算法中属辅助操作，只为了增加种群多样性，不可太大，否则就纯粹随机搜索了，故Pm=0.1。 (2)染色体排序： 首先将各染色体的D位基因值分别代入适应度函数，各得一个适应度函数值，然后利用 sort函数依据适应度函数升序的方式将各染色体排序。 (3)遗传操作及种群合并提取： (3.1)采用君主方案进行选择交叉操作； (3.2)基于概率的变异操作：逐染色体，逐基因进行遍历变异； (3.3)染色体重排序：接下来需要对进行过遗传操作的子种群按照与以上相同方式进 行升序排列。再将排好序的子种群与原排好序的父种群的适应度函数值记忆染色体组均进 行合并，并重新升序排列。取前NP个染色体及其适应度函数值作为优化结果，当然最小的适 应度函数值作为当代最优值。 (4)迭代： 迭代上述过程G次，将G个适应度函数值绘成曲线。 单独执行PSO算法包括如下步骤。 (1)变量初始化： 对于种群规模，设粒子个数N=100，其维数设为D=10，最大迭代次数T=1000；对于加速常 数，也称学习因子c1和c2，决定粒子运行轨迹的个体经验和群体经验，一般设置c1=c2=1.5； 惯性权重可控制粒子向新区域的探索能力和在原区域深度开发的能力设w=0.8时可使该算 法有更快的收敛速度；根据适应度函数要求可确定粒子运动范围，即位置的最大值Xmax=20 和最小值Xmin=-20，另外为了避免粒子飞过优秀区域或是陷入局部最优，设定速度最大值 Vmax=10，最小值Vmin=-10。 (2)种群初始化： 种群初始化包括种群个体，个体最优位置和最优值以及全局最优位置和最优值。个体 包含位置x和速度v两个值，且矩阵x和v等型，均为[N,D]型。对于个体最优位置p，由于刚只 进行了初始化，只需将粒子的初始化位置赋予最优位置p，而个体最优值pbest也是由初始 位置x代入适应度函数求得的。对于全局最优位置g和最优值gbest，将各个个体最优pbest 与全局最优初始值比较，较小者作为全局最优值并将于此对应的个体最优位置作为全局最 优位置。 (3)种群更新： 对种群初始化后，要更新种群并不断进化才可寻优。包括更新个体的最优位置和最优 值，全局最优位置和最优值，各粒子的位置和速度以及边界条件的处理。对于每个粒子都要 做如下更新： (3.1)  个体的最优位置和最优值的更新：将初始化的位置代入适应度函数，将求得的 6 CN 111598209 A 说　明　书 3/10 页 函数值与对应pbest值比较，若该函数值较小，则将该粒子的位置放于对应个体最优位置矩 阵p中,暂当该粒子的个体最优位置，且此时对应的个体最优值pbest也更换为该函数值； (3.2)全局最优位置和最优值的更新：将更换后得到的pbest值与已初始化得到的全局 最优值gbest作比较。若该pbest值小于gbest值，将该pbest值对应的位置放入全局最优位 置矩阵g中，暂当全局最优位置，且此时的gbest值也更换为此gbest值； (3.3)粒子的位置和速度的更新：用如下公式对该粒子的速度和位置做出更新： v(j,:)=w*  v(j,:) c1*rand*(p(j,:)-x(j,:)) c2*rand*(g-x(j,:)); x(j,:)=  x(j,:)   v(j,:); 式中j代表某个粒子，j取(1,N)； 在速度更新公式中，第一部分表示粒子维持原先速度的惯性；第二部分表示粒子向个 体最优位置靠近，即为自我认知；第三部分表示粒子向全局最优位置靠近，即社会引导； (3.4)对边界条件的处理：对于该粒子上的每一位元素（位置、速度），若存在大于最大 速度或小于最小速度的情况，即飞行速度不合理，或若存在大于最大位置或小于最小位置 的情况，即超出了边界，将该位的位置规范进先前的区域内。 (4)遍历： 当所有粒子遍历上述操作一遍后，即完成了一代的更新。将这一代所得的全局最优值 和最优位置记录下来。记录下遍历T代后所得的T个全局最优值并绘制成曲线。 串行式算法融合研究的特征在于，将GA算法进化得出的种群作为PSO算法执行的 初始种群，或将PSO算法迭代出的最优结果作为GA算法的初始种群；如下步骤执行。 (1)先PSO后GA： 初始化部分包括群体粒子个数、染色体数，粒子维数、基因数，粒子群最大迭代次数、遗 传算法最大遗传代数，两个相等的学习因子，限定粒子空间位置的位置最大值、最小值，约 束粒子飞行跨度的速度最大值、最小值，惯性权重，遗传算法的交叉、变异概率以及初始种 群和子种群赋空间。先执行粒子群算法部分，借鉴单独使用PSO的方式，可得到迭代T代后的 粒子群最优位置矩阵p。由于PSO部分与GA部分的初始矩阵互为转置关系，故此处只需要将 PSO优化后得到的最优位置矩阵p转置后作为GA的初始矩阵，即简单实现了PSO与GA的串行 混合，此处的GA部分也与前面单独使用GA部分保持一致。最后将GA迭代了G代后得到的各适 应度值绘制成曲线即可。 (2)先GA后PSO： 对于先遗传算法后粒子群算法，可借鉴以上做法，将单独使用GA部分的执行结果作为 单独执行PSO部分的初始矩阵，也可实现GA与PSO的简单串行混合。 针对已有GA-PSO收敛速度慢等问题，本发明提出的改进GA-PSO，随机初始化的粒 子群个体经改进GA优化一遍直接交由PSO执行，具体改进方法如下步骤执行。 (1)初始化： (1.1)将单个粒子初始位置、速度、最优位置、最优值矩阵合并为A，并按照初始单个粒 子最优值（适应度值）利用sortrows函数将整体升序排列为B； (1.2)将适应度值低的前一半粒子直接放入下一代，将后一半粒子放入Crocs中进行一 系列遗传操作：先是基于概率的交叉操作。若由rand函数随机生成的数小于交叉概率且利 用randint函数生成的一行一列数组中的某位元素为1时，则将后一半粒子两两成对地把元 7 CN 111598209 A 说　明　书 4/10 页 素为1对应位交换，实现基于概率的交叉；再是基于概率的变异操作。将粒子总数与变异概 率的乘积作为迭代上限，并将粒子维数与变异概率之积作为要变异的位数，再利用randint 函数从[1,N/2]和[1,D]中随机选取要变异的粒子体积元素位进行取反变异，反复迭代实现 基于概率的变异操作。 (2)遗传算法优化： 将更换后得到的pbest值与已初始化得到的全局最优值gbest作比较。若该pbest值小 于gbest值，将该pbest值对应的位置放入全局最优位置矩阵g中，暂当全局最优位置，且此 时的gbest值也更换为此gbest值。 (3)Cross部分的更新： (3.1)将进行过交叉变异的位置代入适应度函数中，将其函数值放入Cross中粒子最优 值处，然后与原B中后N/2个粒子的对应值比较；若该函数值小于B中对应值，则将该值对应 的位置放入Cross对应最优位置矩阵，否则将B的该值对应的最优位置放入Cross对应最优 位置矩阵处； (3.2)经过以上更新后，Cross的最优位置矩阵处全部为各粒子的最优位置，再将这些 最优位置代入适应度函数，所得值放入对应最优值处，此时得到Cross的最优位置及最优 值； (3.3)将Cross与B中后半部分进行合并，再次利用sortrows对最优值进行升序排列，将 排序所得前N/2整体投入下一代与原来直接进入下一代的粒子群体组成由GA优化后的粒子 群，也即执行PSO的初始值。 (4)粒子群算法的对接： 执行PSO部分包括去依次迭代更新个体最优位置、最优值，更新全局最优位置、最优值， 更新个体的位置、速度，边界条件的处理以及记录历代全局最优值等，均与上单独执行PSO 部分完全一致。 算法的性能比较往往需要基准函数来验证，本发明选取的基准函数如下： ①Sphere函数： ②Rastrigrin函数： ③Ackley函数： 。 本发明提出的串行式算法融合思想，将GA算法与PSO算法巧妙结合，扬长避短，相 对于单一算法在计算精度、收敛速度、全局稳定性方面均有明显提升；另外针对现有GA-PSO 技术的收敛速度慢的问题，本发明提出的改进GA-PSO，在保证计算精度的基础上，明显提高 了收敛速度。 8 CN 111598209 A 说　明　书 5/10 页 附图说明 图1是实施方式的总体流程图。 图2是实施方式中单独GA算法流程图。 图3是实施方式中单独PSO算法流程图。 图4是实施方式中改进GA(*GA)算法流程图。 图5是五种算法在Sphereh函数上的寻优过程比较。 图6是五种算法在Rastrigrin函数上的寻优过程比较。 图7是五种算法在Ackley函数上的寻优过程比较。