技术摘要：
一种基于伺服进给系统衰放倍率的插补指令评价方法，在数控系统采集输出到机床伺服进给轴的指令位置序列，通过时频变换方法得到相应的指令位置时频图，并提取各个时刻时频图的截面，得到相应的频谱曲线；通过伺服进给系统的闭环传递函数，画出其频谱图，并转换为衰放倍  全部
背景技术：
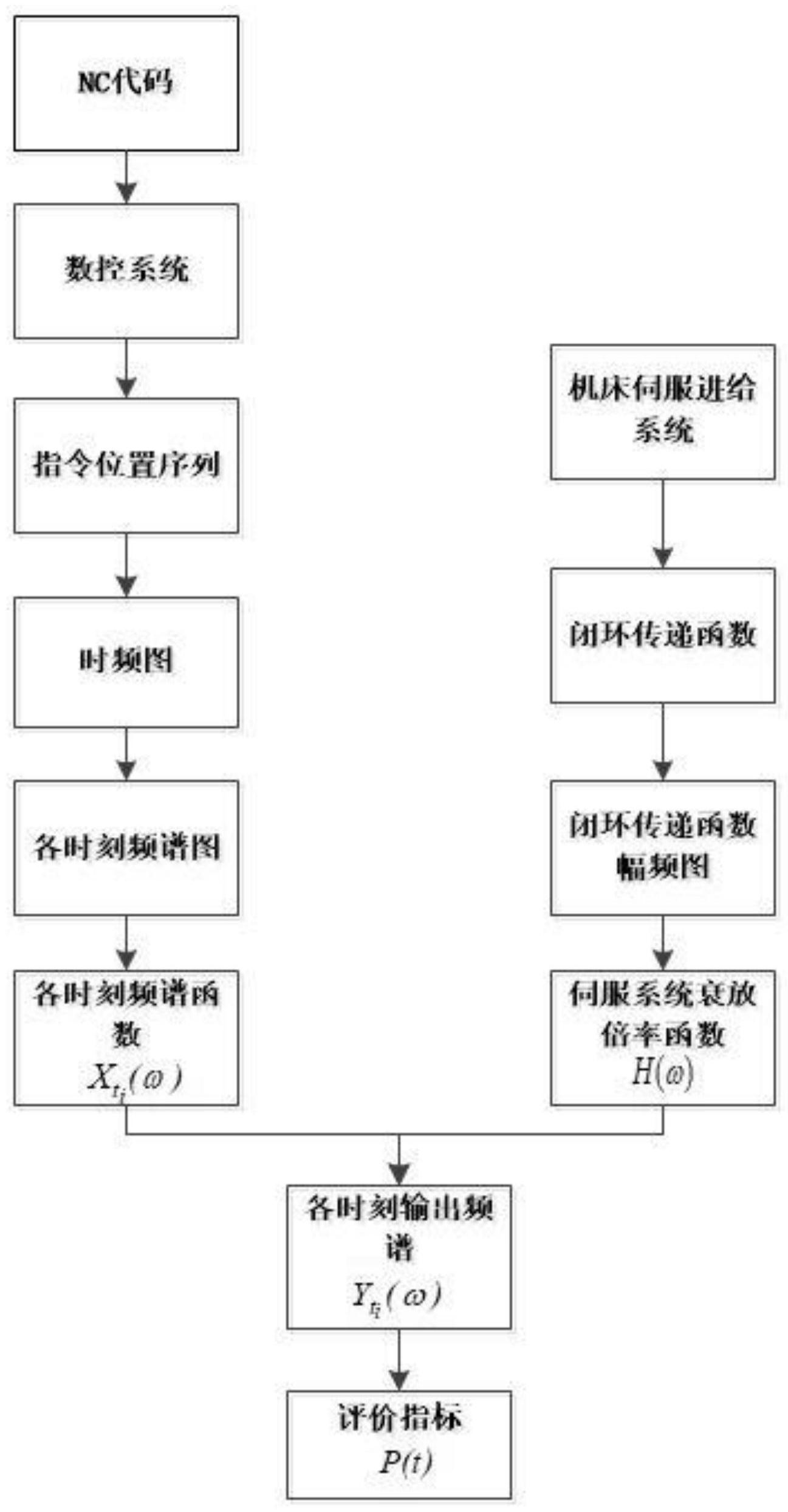
为了克服上述现有技术的缺点，本发明的目的在于提供一种基于伺服进给系统衰 放倍率的插补指令评价方法，能精确地反映跟随精度。 为了达到上述目的，本发明采取的技术方案为： 一种基于伺服进给系统衰放倍率的插补指令评价方法，包括以下步骤： 步骤1.构建插补指令位置序列的时频图： 1.1采集单轴进给运动中数控系统插补输出给伺服进给系统的指令位置序列； 1.2采用时频分析方法，对指令位置序列进行时频变换，构建其时频图； 1 .3在时频图中，截取各个时刻截面，并绘制出各个时刻的频谱图；在ti时刻截面 的频谱图中， 表示幅值随频率ω变化的函数； 步骤2.计算伺服进给系统的衰放倍率： 2.1建立伺服进给系统的闭环传递函数G(s)； 4 CN 111610752 A 说　明　书 2/5 页 2.2绘制闭环传递函数G(s)的幅频图，幅频图的纵坐标为G(s)的幅值G|jω|，横坐 标为频率ω，根据幅频图，构建衰放倍率随频率变化的函数H(ω)，如公式(1)所示； H(ω)＝|G(jω)|  ω∈(0, ∞)    (1) 绘制倍率函数H(ω)随频率ω的变化曲线； 步骤3.构建经伺服进给系统衰放后的指令各个时刻截面频谱图： 在某时刻ti，由公式(2)得到指令频谱函数 经过伺服进给系统衰放后的输 出频谱函数 式中，“×”表示两函数 和H(ω)相乘； 在同一频谱图中绘制 的函数曲线； 步骤4.计算某时刻ti指令被伺服进给系统衰放的占比P(ti)： ti时刻， 函数曲线在其频谱中的面积为： ti时刻，指令被 伺服进给系统衰放的部分在频谱中的面积为： 计算ti时刻，指令被伺服进给系统衰放的占比P(ti)，公式如式(3)所示； 步骤5.计算整个刀具路径上各个时刻指令被伺服进给系统衰放的占比P(t)： 按照步骤3-4，计算各个时刻指令被伺服进给系统衰放的占比P(ti)后，建立指令 被伺服进给系统衰放的占比随时间变化的曲线P(t)；将指令输入伺服进给系统，得到跟随 误差。 所述的步骤2.2中当函数H(ω)的值大于1，表示指令输入伺服进给系统后的输出 会被放大，各个频率ω上幅值的放大倍数即为H(ω)；当H(ω)的值小于1，表示指令输入伺 服进给系统后的输出会被衰减，各个频率ω上幅值的衰减倍数即为H(ω)；当H(ω)等于1， 表示既没放大，也没衰减。 所述的步骤3中在同一频谱图中绘制 的函数曲线， 函数 和函数 构成两条函数曲线， 函数曲线低于 的 频率ω区域，对应指令频率输入伺服进给系统后的输出幅值被衰减； 函数曲线高于 的区域，对应指令频率输入伺服进给系统后的输出幅值被放大；指令输入伺服进给 系统后的输出无论被放大还是衰减，均会造成输出相对于输入的偏差，造成伺服进给系统 的跟随误差； 5 CN 111610752 A 说　明　书 3/5 页 若 和 两函数曲线重合，对应指令频率输入伺服进给系统后的输出 幅值不会被衰减或放大，则不会产生伺服进给系统的跟随误差。 所述的步骤4中P(ti)的大小表示了ti时刻指令被伺服进给系统衰放的大小，P(ti) 越大，指令衰放量越大，则跟随误差越大。 所述的步骤5中P(t)的取值范围为0-1,在某时刻t，取值越小表明该时刻的跟随误 差越小，取值越大，表明该时刻的跟随误差越大； P(t)随时间的变化，反映不同刀具路径位置即不同时刻跟随误差的差异。 本发明具有以下有益效果为： 本发明结合数控插补指令和机床伺服进给系统的特性，可以评价机床伺服进给系 统对数控插补指令的响应能力，以此为插补指令优化和伺服进给系统性能的改善提供依 据。 附图说明 图1为本发明的流程图。 图2为本发明实施例指令位置序列的时频图。 图3为本发明实施例某时刻时频图截面图。 图4为本发明实施例衰放倍率图。 图5为本发明实施例某时刻指令衰放频谱和原始指令频谱。 图6为本发明实施例评价指标随时间变化的曲线图。 图7为本发明实施例跟随误差图。
技术实现要素：
下面结合附图和实施例对本发明做详细描述，本实施例以数控机床某进给轴的折 返运动为例。 参照图1，一种基于伺服进给系统衰放倍率的插补指令评价方法，包括以下步骤： 步骤1.构建插补指令位置序列的时频图： 1.1采集单轴折返运动中数控系统插补输出给伺服进给系统的指令位置序列； 1 .2采用时频分析方法，对指令位置序列进行时频变换，构建其时频图，如图2所 示； 1.3在时频图中，截取各个时刻截面，并绘制出各个时刻的频谱图，如图3所示，图3 为ti＝1.064s时刻的时频图截面， 表示该时刻频谱图中，幅值随频率ω变化的 函数； 步骤2.计算伺服进给系统的衰放倍率： 2.1建立伺服进给系统的闭环传递函数G(s)； 2.2绘制闭环传递函数G(s)幅频图，幅频图的纵坐标为G(s)的幅值G|jω|，横坐标 为频率ω，根据幅频图，构建衰放倍率随频率变化的函数H(ω)，如公式(1)所示， H(ω)＝|G(jω)|  ω∈(0, ∞)    (1) 当函数H(ω)的值大于1，表示指令输入伺服进给系统后的输出会被放大，各个频 6 CN 111610752 A 说　明　书 4/5 页 率ω上幅值的放大倍数即为H(ω)；当H(ω)的值小于1，表示指令输入伺服进给系统后的输 出会被衰减，各个频率ω上幅值的衰减倍数即为H(ω)；当H(ω)等于1，表示既没放大，也没 衰减； 绘制倍率函数H(ω)随频率ω的变化曲线，即衰放倍率图，如图4所示； 步骤3.构建经伺服进给系统衰放后的指令ti＝1.064s时刻截面频谱图： 在ti＝1.064s，由公式(2)可得指令频谱函数 经过伺服进给系统衰放后的 输出频谱函数 式中，“×”表示两函数 和H(ω)相乘； 在同一频谱图中绘制 的函数曲线，如图5所示；函数 和 函数 构成两条函数曲线， 函数曲线低于 的频率ω区域，对应指令频率 输入伺服进给系统后的输出幅值被衰减； 函数曲线高于 的区域，对应指令频 率输入伺服进给系统后的输出幅值被放大；指令输入伺服进给系统后的输出无论被放大还 是衰减，均会造成输出相对于输入的偏差，造成伺服进给系统的跟随误差； 若 和 两函数曲线重合，对应指令频率输入伺服进给系统后的输出 幅值不会被衰减或放大，则不会产生伺服进给系统的跟随误差； 步骤4.计算某时刻ti指令被伺服进给系统衰放的占比P(ti)： ti时刻，函数曲线 在其频谱中的面积为： ti时刻，指令被伺服进给系统衰放的部分在频谱中的面积为： 计算ti时刻，指令被伺服进给系统衰放的占比P(ti)，公式如式(3)所示； P(ti)的大小表示了ti时刻指令被伺服进给系统衰放的大小，P(ti)越大，指令衰放 量越大，则跟随误差越大； 步骤5.计算整个刀具路径上各个时刻指令被伺服进给系统衰放的占比P(t)： 按照步骤3-4，计算各个时刻指令被伺服进给系统衰放的占比P(ti)，建立从时间0 秒到8.9260秒指令被伺服进给系统衰放的占比随时间变化的曲线P(t)，如图6所示； P(t)的取值范围为0-1,在某时刻t，取值越小表明该时刻的跟随误差越小，取值越 大，表明该时刻的跟随误差越大； P(t)随时间的变化，反映不同刀具路径位置即不同时刻跟随误差的差异。 7 CN 111610752 A 说　明　书 5/5 页 将指令输入伺服进给系统，得到跟随误差，如图7所示。 8 CN 111610752 A 说　明　书　附　图 1/4 页 图1 9 CN 111610752 A 说　明　书　附　图 2/4 页 图2 图3 10 CN 111610752 A 说　明　书　附　图 3/4 页 图4 图5 11 CN 111610752 A 说　明　书　附　图 4/4 页 图6 图7 12